Wladimir Lyra
Associate Professor
New Mexico State University
Department of Astronomy
PO Box 30001, MSC 4500 Las Cruces, NM 88003
wlyra - nospam - nmsu.edu
+1 575-646-1400
Menu:
Disk turbulence
Rossby wave instability
As accretion in protoplanetary disks is enabled by turbulent
viscosity, the border between active and inactive (dead) zones
constitutes a location where there is an abrupt change in the
accretion flow. The gas accumulation that ensues constitutes a
localized pressure bump, that behaves as a resonant cavity. Waves are
trapped in this cavity if the density transition is sufficiently
sharp. For a smooth jump the waves will tunnel away, but for sharp,
high amplitude jumps, bound states exist. In resonance, the wave amplitudes will
grow exponentially. The saturated state are anticyclonic vortices.
The movie below show the transition between MRI active (outer disk)
and MRI dead (inner disk) zones. The transition is as smooth as 15
scale heights in resistivity (from 10-30 AU), following the smooth decrease
in ionization due to attenuation of stellar X-rays. At some point the
Lundquist number drops rises above 1 and the MRI is abruptly triggered
(irrespectively of how smooth the resistivity jump is). Notice a
Rossby vortex forming in the transition (the yellowish
non-axisymmetric structure at the transition zone by the end of the
simulation).
This simulation is the first to show that a smooth jump
in resistivity can still trigger the RWI. Previous alpha disks models
(Lyra et al. 2009a) suggested that only jumps sharper than 2H would do the trick.
|
Publication: Lyra et al. (2014), A&A, accepted. [arXiv] |
The model below was the first model of the RWI with a properly modeled
active zone. By that we mean with MRI in a MHD disk instead of
viscosity jumps in an alpha disk. It represents the transition from
the inner active zone to the dead zone, at 0.1 AU, when temperature
drops below 900K and collisions are not energetic enough to ionize
the alkali metals.
|
Publication: Lyra & Mac Low (2012), ApJ, 756, 62.[arXiv] [ADS] |
Convective overstability
A hydrodynamical linear overstability exists in protoplanetary
disks, powered by buoyancy in the presence of thermal relaxation.
We model the system numerically, reproducing the linear growth
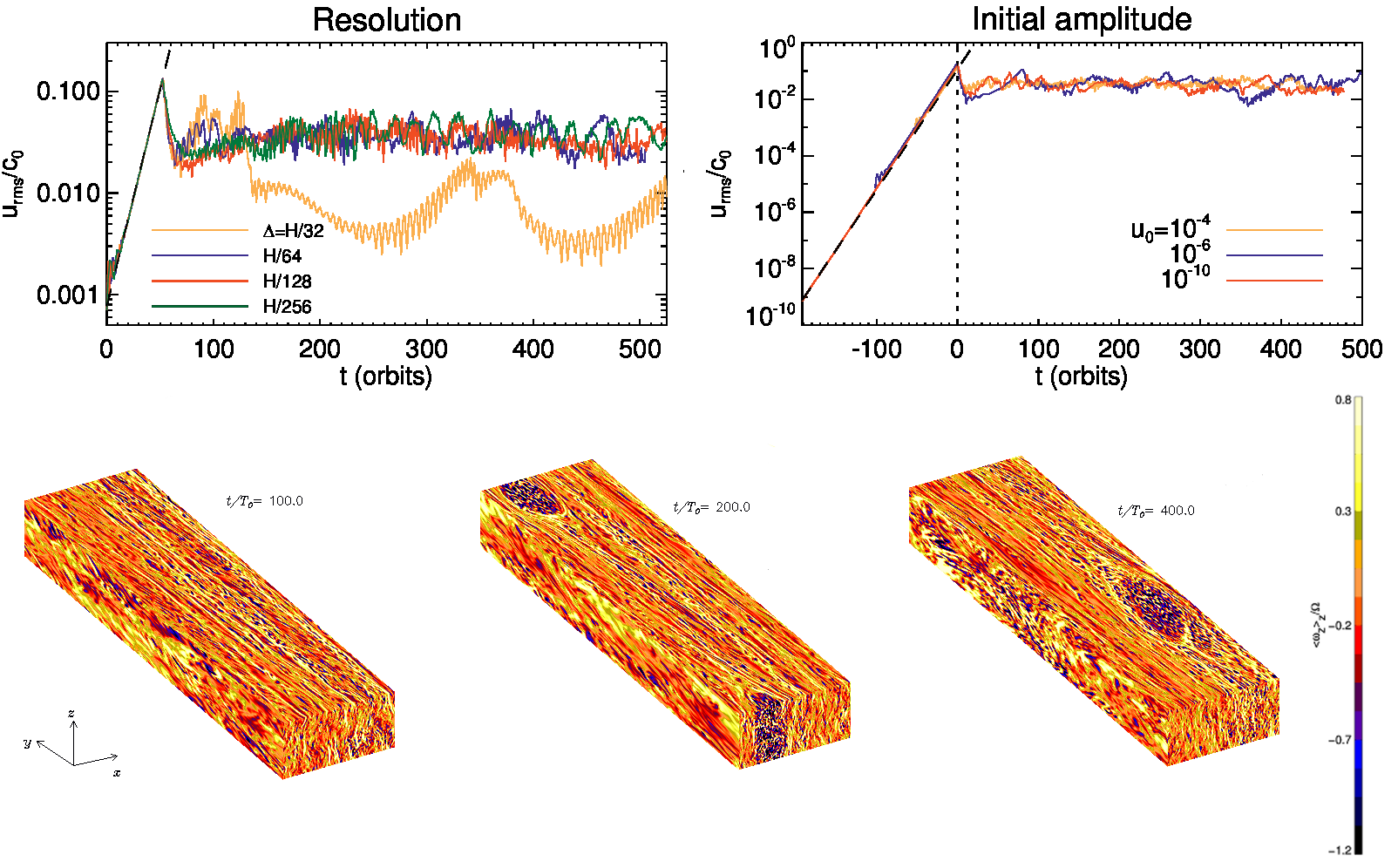
rate for all cases studied. The figure shows the linear and nonlinear
evolution of the overstability. Upper panels: Convergence study with
resolution (left) and initial amplitude of perturbation
(right). Resolution of 64 points per scale height is enough to resolve
the overstability, and initial amplitudes as small as sound speed (c0) are enough to lead to growth, demonstrating the
linear nature of the process. The linear growth rate (black dashed
curve) is well reproduced in all cases. Lower panels: With the linear
overstability raising the amplitude of the initial fluctuations to
nonlinear levels, a large-scale vortex is generated in the course of
the next 100 orbits. This was the first simulation
that generated a self-sustained 3D vortex from linear amplitude
perturbation of a quiescent base state.
Publication: Lyra (2014), ApJ, 789, 77. [arXiv]
[ADS]
Before the linearity of the instability had been recognized (Klahr &
Hubbard 2014), however, much about the saturated state had been
deduced, yet under the assumption that the instability was nonlinear
in nature. We used to call it "baroclinic instability", for
reasons that have nothing to do with atmospheric physics. It is a
misnomer that was around for long enough to make it to a
number of publications. To discriminate between that and the
geophysical one, we call the former "subcritical baroclinic
instability" (SBI) nowadays, following suggestion by Geoffroy
Lesur. So, the saturated state of the COS is the SBI. The movie shows
the development of the SBI (BI) in a 2D local shearing box model. The
box used was small, and only one vortex remained. In general, vortices
do not grow past the sonic scale, as they shock, radiating excess
vorticity and thus shrinking. The SBI is shown to provide a hydrodynamical source of turbulence, allowing for some degree of accretion (alpha of the order of 5e-3) in the absense of magnetization.
|
Publications: Lyra & Klahr (2011), A&A, 527, 138. [arXiv] [ADS] Publications: Raettig et al. (2013), ApJ, 765, 115. [arXiv] [ADS] |
Magneto-elliptic instability
Phenomenologically, turbulence can be described as a series of bifurcations, starting with a primary instability that converts shear into vorticity, creating vortices. This is followed by another bifurcation, a secondary instability, to break these vortices into lesser vortical structures. These in turn shall experience a sequence of inertial instabilities, leading to a cascade. Though the Kelvin-Helmholtz instability and the Rayleigh-Taylor instability are well established as examples of primary instabilities, the highly successful theory of the turbulent cascade put forth by Kolmogorov rested on a heuristic picture of secondary instability, established by early experiments. It was not until the 80s that the elliptic instability was introduced as a mechanism for secondary instability. A fluid in rigid rotation supports a spectrum of stable inertial waves, the simplest case being circularly polarized transverse plane waves oscillating at twice the frequency of the base flow. Strain is introduced when the streamlines pass from circular to elliptical, and some modes find resonance with the strain field, leading to de-stabilization. This is called "elliptic instability".
In this simulation we examined the magnetic properties of vortices produced by the SBI. When magnetic fields are introduced in the problem, the addition of Alfven waves enriches the families of unstable modes. When background rotation is introduced, the same as had occurred to the elliptic instability en- sues. When this background rotation runs opposite to the rotation of the vortex (anti-cyclonic motion), a fluid parcel becomes subject to an intense effective shear. Since the magnetic tension resists shear, leading to instability a powerful unstable in-plane mode appears. This instability is of course the magneto-rotational instability, in generalized form. This provides an interesting unification, explaining the magneto-elliptic and magneto-rotational instabilities as different manifestations of the same magneto-elliptic-rotational instability
We find that vortices survive the hydrodynamical elliptic instability, but they fall prey to the more violent
magneto-elliptic instability. The conclusion is that vortices are restricted to the dead zones of accretion disks.

|
Publications: Lyra & Klahr (2011), A&A, 527, 138. [arXiv] [ADS] Publications: Mizerski & Lyra (2012), JFM, 698, 358. [arXiv] [ADS] |
Transitional disks
The Atacama Large Millimeter Array (ALMA) has been returning images of transitional disks in which large asymmetries are seen in the distribution of mm-sized dust in the outer disk. The explanation in vogue borrows from the vortex literature by suggesting that these asymmetries are the result of dust trapping in giant vortices, excited via Rossby wave instability (RWI) at planetary gap edges. Due to the drag force, dust trapped in vortices will accumulate in the center, and diffusion is needed to maintain a steady state over the lifetime of the disk. While previous work derived semi-analytical models of the process, in this paper we provide analytical steady-state solutions. Exact solutions exist for certain vortex models. The solution is determined by the vortex rotation profile, the gas scale height, the vortex aspect ratio, and the ratio of dust diffusion to gas-dust friction. In principle, all these quantities can be derived from observations, which would give validation of the model, also giving constrains on the strength of the turbulence inside the vortex core. Based on our solution, we derive quantities such as the gas-dust contrast, the trapped dust mass, and the dust contrast at the same orbital location. We apply our model to the recently imaged Oph IRS 48 system, finding values within the range of the observational uncertainties.
Publication: Lyra & Lin 2013.
Photoelectric instability
Structure seen in debris disks - sharp rings, eccentricities, asymmetric ansae - are usually taken as evidence for the gravitational influence of unseen planets, as these disks are mostly gas-free systems of dust and leftover planetesimals. In this simulation we show that if the system has gas, hydrodynamical forces at work suffice to explain the structure seen in debris disks. This gas comes from outgassing of planetesimals and dust grains via sublimation, photodesorption, or collisions, generating a system of dust-to-gas ratio close to unity, where hydrodynamics cannot be ignored. The backreaction of the drag force from the gas onto the dust shepherds rings. The eccentricity can be simply explained by a standing wave propagating along the ring. The planet possibility, though thrilling, is not necessarily required to explain these systems.
Publication: Lyra & Kuchner 2013.