Wladimir Lyra
Associate Professor
New Mexico State University
Department of Astronomy
PO Box 30001, MSC 4500 Las Cruces, NM 88003
wlyra - nospam - nmsu.edu
+1 575-646-1400
Menu:
Disk migration
My work on migration is divided between protoplanetary disks, to explain the survival of the Earth against angular momentum loss to the gas disk; and AGN disks, to explain the recent LIGO observations of black hole binary mergers. These works are detailed below.
Planet migration in evolutionary disk models
In this series of works, I am interested in the final orbit of planets, as a result
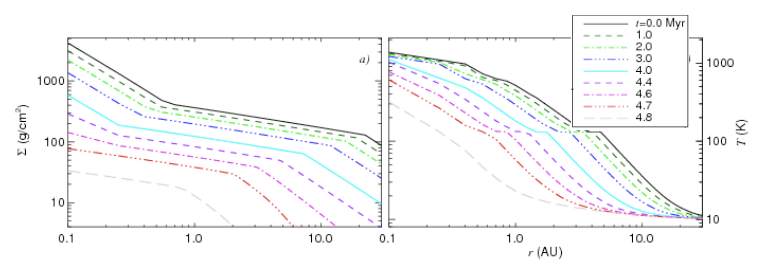
of migration and disk evolution. As the gas accretes and photo-evaporates, the
density (LHS figure) and temperature (RHS picture) fall steadily.
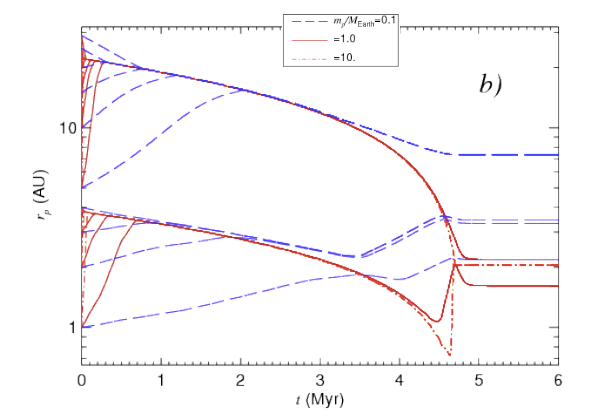
Planet migration occurs towards equilibrium radii with zero torque. These
radii themselves migrate inwards as the disk evolves. We see that as
the surface density and temperature fall, the planet orbital migration
and disk depletion timescales eventually become comparable, with the
precise timing depending on the mass of the planet. When this occurs,
the planet decouples from the equilibrium radius. At this time,
however, the gas surface density is already too low to drive
substantial further migration. A higher mass planet, of 10 Earth
masses, can open a gap during the late evolution of the disk, and
stops migrating. Low mass planets, with 1 or 0.1 Earth masses,
released beyond 1 AU in our models, avoid migrating into the star.
|
In the video below we take this model one step further by implementing
multiple interacting planets. We incorporate the
torques from an evolving non-isothermal disk into an N-body simulation
to examine the behavior of planets or planetary embryos interacting in
the convergence zone. We find that mutual interactions do not eject
objects from the convergence zone. Small numbers of objects in a
laminar disk settle into near resonant orbits that remain stable over
the 10 Myr periods that we examine. However, either or both increasing
the number of planets or including a correlated, stochastic force to
represent turbulence drives orbit crossings and mergers in the
convergence zone. These processes can build gas giant cores with
masses of order ten Earth masses from sub-Earth mass embryos in 2-3
Myr. This simulation and video were done by Brandon Horn, the graduate
student at Columbia University, with my co-supervision.
Horn et al. (2012), ApJ, 750, 34. [arXiv] [ADS]
Lyra et al. (2010), ApJ, 715, L68. [arXiv] [ADS]
Black hole migration and merger in AGN disks
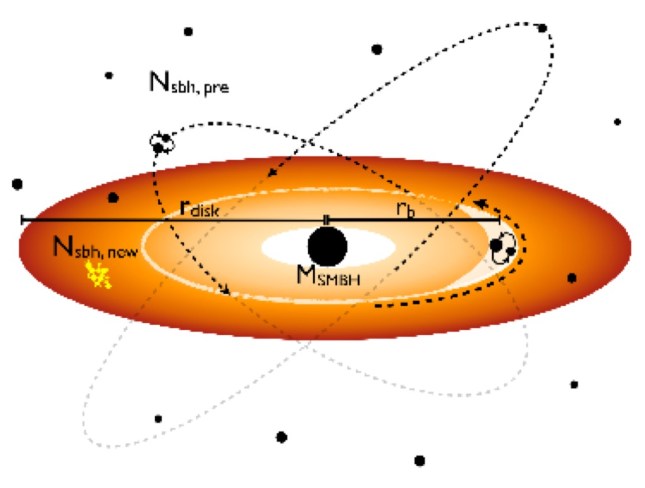
I have been participating in a collaboration with the goal of explaining the LIGO observations as merger events in AGN, similarly to the core accretion model in protoplanetary disks. The idea is based on the realization that the mass ratio of compact objects or stellar mass black holes (1-10 solar masses) to a supermassive black hole (1e6-1e8 solar masses) is about the same as that of planetesimals/protoplanets to the Sun. Thus, in the same way that planetesimals in a protoplanetary disk collide to form protoplanets and planets, stellar mass black holes orbiting in an AGN disk would collide to form larger black holes. Essentially, the core accretion model of planet formation can be scaled up to AGN disks. The presence of gas in the AGN makes the motion dissipative, so black holes will migrate in the same way planets migrate in circumstellar disks. Hefty black holes like seen by LIGO are difficult to explain by stellar evolution, but would be natural outcomes of this model. We have published a series of works dealing with key aspects of the model.
Publications:
Secunda et al. (2018) ApJ, submitted.[arXiv]
McKernan et al. (2018), ApJ, 866, 66.
[arXiv]
[ADS]
Leigh et al. (2018), MNRAS, 474, 5672.
[arXiv]
[ADS]
Bellovary et al. (2016), ApJL, 819, L17.
[arXiv]
[ADS]
McKernan et al. (2014), MNRAS, 441, 900.
[arXiv]
[ADS]
McKernan et al. (2012), MNRAS, 425, 460.
[arXiv]
[ADS]
McKernan et al. (2011), MNRAS, 417L, 103.
[arXiv]
[ADS]