Menu:

Planet Formation

The current paradigm in planet formation theory is developed around a hierarchical growth of solid bodies, from interstellar dust grains to rocky planetary cores. A particularly difficult phase in the process is the growth from cm-sized pebbles to planetary embryos of the size of our Moon or Mars. Subject to angular momentum loss through nebular drag, peebles are expected to drift extremely rapid in a protoplanetary disk, so that they would generally fall into the central star well before larger bodies can form.

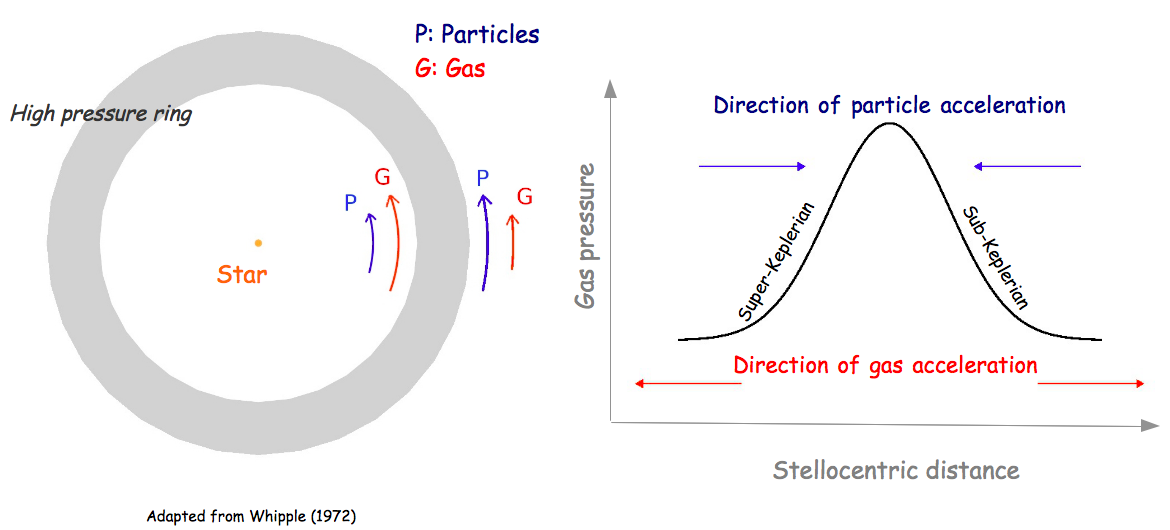
Ways around this problem have focused on the development of pressure traps in the disk. The way these pressure traps work are shown in the figures below. While a negative pressure gradient slows down the gas, a positive one speeds it up. Particles thus feel a headwind in a negative pressure gradient, and a tailwind in a positive one. The result is that particles drift toward pressure maxima.  

 
 

 
Turbulence is a way to generate several of such pressure maxima. The simulation below shows the saturated state of turbulence brought about by magnetorotational instability (MRI) in a 3D stratified wedge of a protoplanetary disk. The quantity shown in the ratio of thermal to magnetic pressure (known as "plasma beta").  

 

 

 
The movie below shows the behaviour of boulders in MRI turbulence. Structure forms as several transient high pressure regions form as a result of the turbulence, trapping particles in them. The color code refers to the bulk density of solids. The bright (yellow-white) is saturated, meaning that these areas are much denser than they appear.  

 

Publication: Lyra et al. 2008a, A&A, 479, 883. [arXiv] [ADS]
 

 
But turbulence is not present throughout the whole extent of the disk. Because sufficient ionization is a main requirement, a significant portion of the cold, dense disk, will be neutral and therefore unmagnetized. In this region, the disk will be "dead" to the MRI and we can expect laminar motion. At the boundary between active and dead zone, however, the transition in turbulent viscosity will trigger Rossy wave instability (RWI), the form that the Kelvin-Helmholtz instability takes in differentially rotating disks. 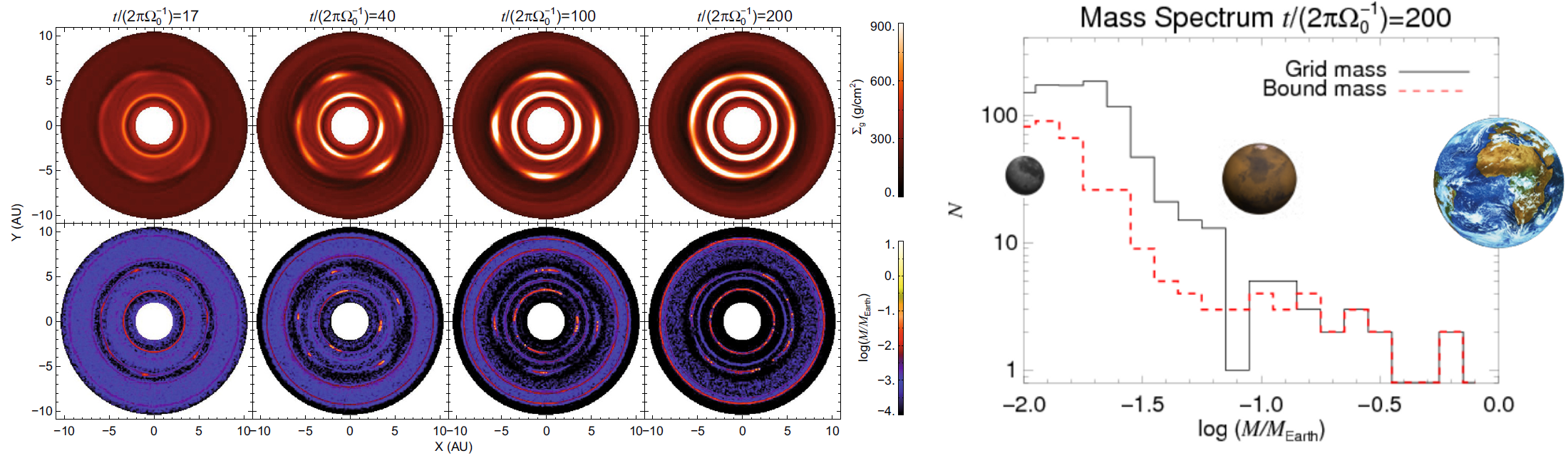The saturated state of the RWI are vortices, that are very effective in concentrating particles. The figure below shows the particle concentration that results from vortex trapping in this scenario. It leads, in this model, to the formation of over three hundred bound clumps of particles -- 20 of them more massive than Mars.  

 

Publications: Lyra et al. 2008b, A&A, 491, L41.[A&A highlight] [arXiv] [ADS]
Publications: Lyra et al. 2009a, A&A, 497, 869. [arXiv] [ADS]  

 
In the video below, a Jupiter-mass planet is perturbing a planetesimal disk of meter-sized bodies. Particles are trapped in the Lagrangian points of the planet and at the border of the gas gap, where large vortices form. In 50 orbits the particles achieve critical density and collapse. The mass attained by the most massive planet is around 5 Earth masses.  

 


Publication: Lyra et al 2009b, A&A, 493, 1125.
[A&A cover] [arXiv] [ADS]
 

 

Disk vortices

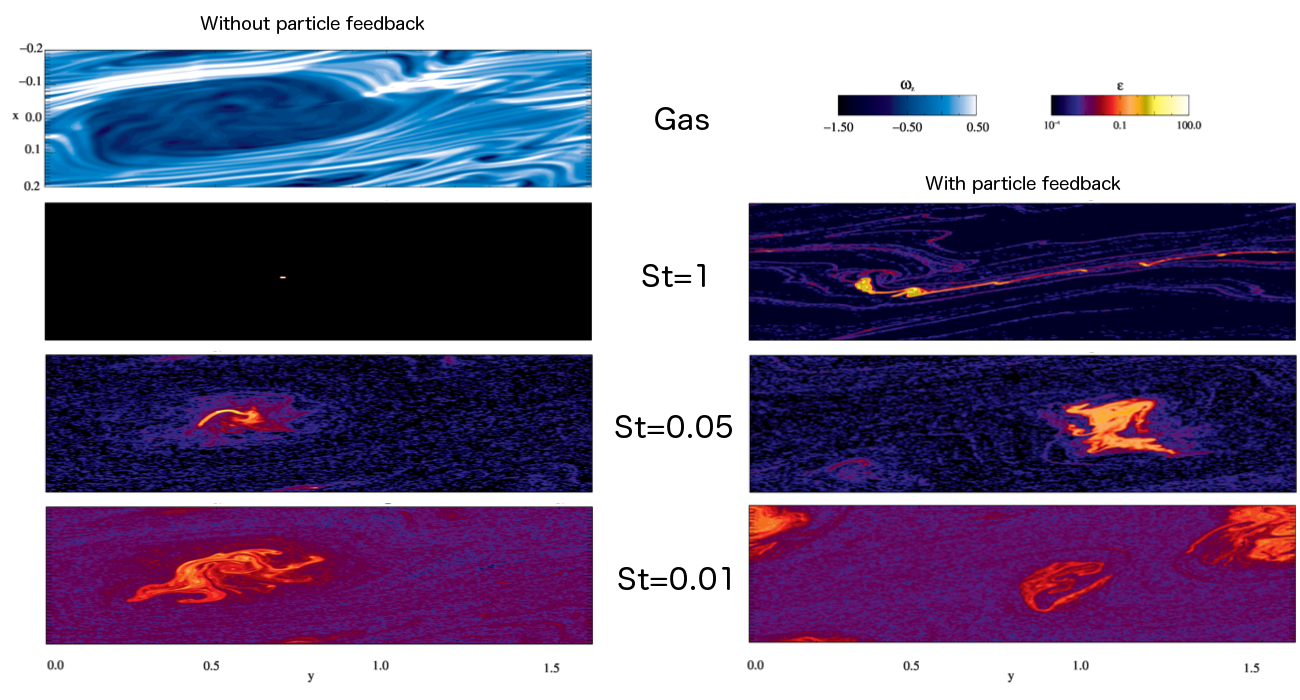
Vortices are hydrodynamical features similar to the Great Red Spot. Long hypothesized to occur in protoplanetary disks, vortices have two properties that make them attractive locations for planet formation. The first is that they are equilibrium solutions to the equations of hydrodynamics, which makes them persistent structures. The second is that under the influence of the drag force, solid bodies inside a vortex experience a radial net force, making them sink to its center. This has the convenient side effect of dramatically enhancing the solids-to-gas ratio locally.

The image below is a high resolution model of 2D vortices in disks, with particles. The upper left panel shows the vorticity in the gas phase. The lower left panels the particles in a model without drag force backreaction; the right panel includes backreaction (which becomes important as St approaches 1). Reproduced from the thesis work of Natalie Raettig, with my co-supervision (Raettig, 2013; also Raettig et al. 2013, 2015).