Wladimir Lyra
Associate Professor
New Mexico State University
Department of Astronomy
PO Box 30001, MSC 4500 Las Cruces, NM 88003
wlyra - nospam - nmsu.edu
+1 575-646-1400
Menu:
Research
This page is currently being revamped. Follow the publications tab for my full list of papers. Check also this link for the work of our extended collaboration PFITS+: Planet Formation in the Southwest
 At Stampede's dedication, Austin TX, April 2013. Each of these towers has 3,000 processors.
At Stampede's dedication, Austin TX, April 2013. Each of these towers has 3,000 processors.
My research focuses on planet formation. You can find here brief explanations of the research highlights, and links to the respective publications.
- Reviews
- Kuiper belt objects
- Pebble Accretion
- Streaming Instability
- Vortex Trapping
- Cyclogenesis
- Photoelectric Instability
- Planet migration
- Planetary shocks
- Code Development
- Magnetorotational Instability
- Observational
- Positional Astronomy
- Educational
- Outreach
Reviews
The dynamical state of the protoplanetary disk is the fundamental canvas where the planet formation narrative is etched. For decades, the mechanism of accretion has been elusive. The magnetorotational instability, thought to be responsible for accretion in magnetized disks, is rendered mostly inoperative in protoplanetary disks, as these disks are dense and cold, lacking sufficient ionization. Hence, the search for hydrodynamical sources of turbulence continues. The problem of accretion is intimately connected to planet formation as well, since planet formation starts with mechanical aerodynamical concentration of pebbles. The decade of the 2010s saw the emergence of three possible mechanisms for generating turbulence: the Vertical Shear Instability, the Convective Overstability, and the subcritical Resonant Buoyant Instability (nee "zombie" vortex instability), which operate in well-separated regimes of opacity. In this review, we summarize the properties of these processes, identify their limitations, and discuss where and under what conditions these processes are active in protoplanetary disk.
Publication: Lyra & Umurhan (2019), PASP, 131, 2001. The Initial Conditions for Planet Formation: Turbulence Driven by Hydrodynamical Instabilities in Disks around Young Stars [ADS]
Kuiper belt objects
The Kuiper belt is a gold mine of information of planetesimal formation. In fact, it is the only place in the Solar System where a population of
pristine planetesimals, the cold classicals, remains extant to this day. The flyby of Arrokoth in 2019 by the New Horizons gave us
detailed constraints on what to expect from the process. Surprisingly, Arrokoth turned out to be a contact binary planetesimal.
I produced a model that explains the orbital
evolution of the individual lobes into contact with a combination of Kozai-Lidov oscillations and gas drag. The code I developed to solve the
combined action of Kozai, induced and permanent tides, and drag (KTJD), is available for download here.
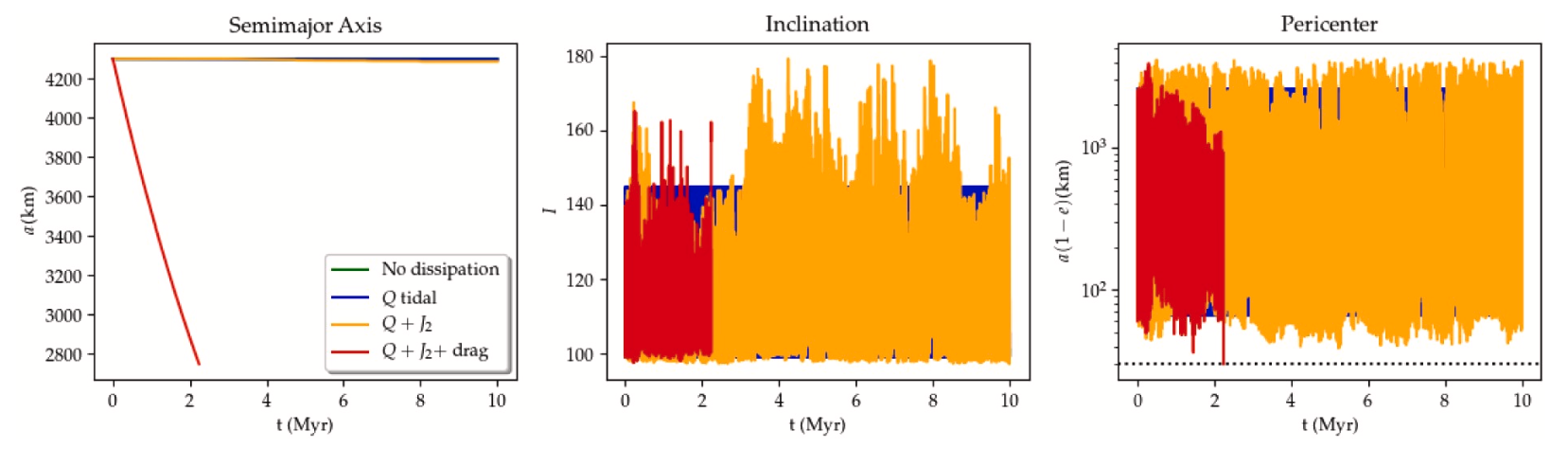 The figure above shows the evolution of the lobes of Arrokoth up to 10 Myr, for simulations with different dynamical terms. The simulation with only the solar terms (green) leads to regular Kozai
oscillations at constant semimajor axis. Including the induced quadrupole (blue) has little effect. Inclusion of the permanent quadrupole (orange) leads to
irregular Kozai cycles with erratic excursions in inclination and eccentricity. Finally, including the orbital drag leads to a fast decay of semimajor axis, and eventual
contact shortly after 2 Myr.
The figure above shows the evolution of the lobes of Arrokoth up to 10 Myr, for simulations with different dynamical terms. The simulation with only the solar terms (green) leads to regular Kozai
oscillations at constant semimajor axis. Including the induced quadrupole (blue) has little effect. Inclusion of the permanent quadrupole (orange) leads to
irregular Kozai cycles with erratic excursions in inclination and eccentricity. Finally, including the orbital drag leads to a fast decay of semimajor axis, and eventual
contact shortly after 2 Myr.
Publication: Lyra, Youdin, & Johansen (2021), Icarus, 356, 113831. Evolution of MU69 from a binary planetesimal into contact by Kozai-Lidov oscillations and nebular drag [ADS]
Another problem I've been concerned about is what information on the planet formation process we can derive from the density of Kuiper belt objects. Density has been measured for a number of objects, for which dynamical mass can be measured (because the objects are binaries), and radii are measured via occultation or thermal radiometry. The pattern that emerges is a bimodal population of low-density low-mass objects, with density gradually increasing toward high-mass objects. I've worked out a solution for this pattern via 1) ice photodesorption off small grains maintains a compositional gradient with radii for the pebbles, with the larger pebbles being shielded and keeping the ice, whereas the small grains preferentially lose ice as they are lofted in the disk atmosphere and get exposed to stellar UV. 2) streaming instability forms planetesimals from the largest pebbles, primarily icy. Finally 3) at this mass range, pebble accretion will preferentially accrete the small pebbles, which are ice-poor in comparison. This solution also avoids the timing problem that ensues if the objects form with too rocky a composition from the outset (the abundance of 26Al would melt the planetesimals).
Publication: Canas & Lyra, et al. (2024), PSJ, 5, 55. A Solution for the Density Dichotomy Problem of Kuiper Belt Objects with Multispecies Streaming Instability and Pebble Accretion
[ADS]
Finally, why is there a mass gap between the low-mass and high-mass objects? This gap is really telling us something profound about planet formation. The low-mass side is consistent with the outcome of planetesimal formation, quenched at 400 km. The objects are
wide binaries of equal brightness, thus easy to find. The high-mass objects, on the other hand, have small satellites in tight orbits. While the gap itself is probably an observational bias, this hints at an architectural dichotomy imprinted by the pebble accretion
process.
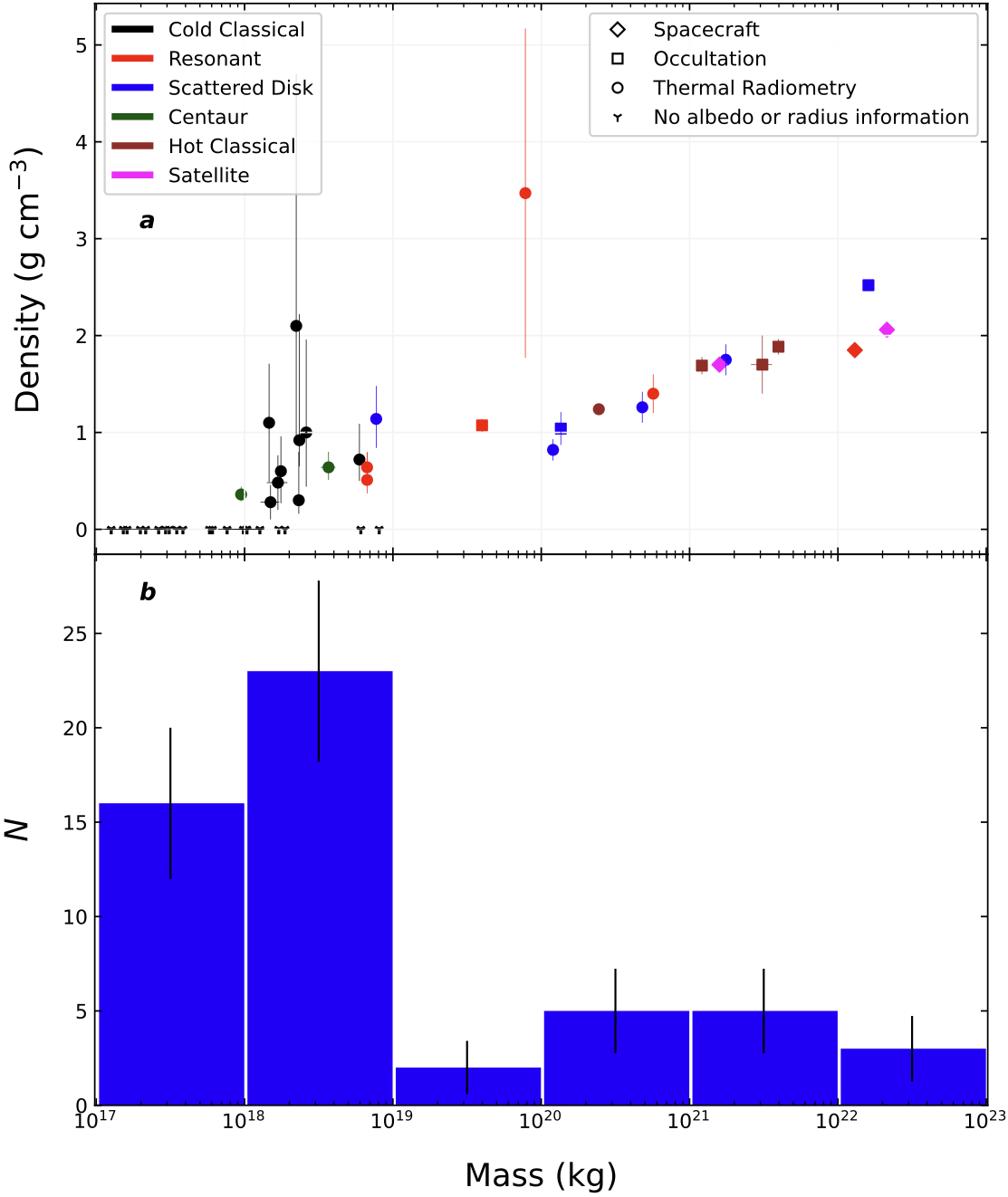
Publication: Lyra (2025), Icarus, 442, 116737. Where are the missing Kuiper Belt binaries? [ADS]
Pebble Accretion
An Analytical Theory for the Growth from Planetesimals to Planets by Polydisperse Pebble Accretionhttps://ui.adsabs.harvard.edu/abs/2023ApJ...946...60L/abstract
Streaming Instability
On the Mass Budget Problem of Protoplanetary Disks: Streaming Instability and Optically Thick Emissionhttps://ui.adsabs.harvard.edu/abs/2025arXiv250610435G/abstract
Vortex Trapping
Rapid Protoplanet Formation in Vortices: Three-dimensional Local Simulations with Self-gravityhttps://ui.adsabs.harvard.edu/abs/2024ApJ...970L..19L/abstract
Vortex solution in elliptic coordinates
https://ui.adsabs.harvard.edu/abs/2021RNAAS...5..180L/abstract
Pebble Trapping in Vortices: Three-dimensional Simulations
https://ui.adsabs.harvard.edu/abs/2021ApJ...913...92R/abstract
Pebble-trapping Backreaction Does Not Destroy Vortices
https://ui.adsabs.harvard.edu/abs/2018RNAAS...2..195L/abstract
Steady State Dust Distributions in Disk Vortices: Observational Predictions and Applications to Transitional Disks
https://ui.adsabs.harvard.edu/abs/2013ApJ...775...17L/abstract
Planet formation bursts at the borders of the dead zone in 2D numerical simulations of circumstellar disks
https://ui.adsabs.harvard.edu/abs/2009A%26A...497..869L/abstract
Standing on the shoulders of giants. Trojan Earths and vortex trapping in low mass self-gravitating protoplanetary disks of gas and solids
https://ui.adsabs.harvard.edu/abs/2009A%26A...493.1125L/abstract
Embryos grown in the dead zone. Assembling the first protoplanetary cores in low mass self-gravitating circumstellar disks of gas and solids
https://ui.adsabs.harvard.edu/abs/2008A%26A...491L..41L/abstract
Cyclogenesis
Rossby wave instability does not require sharp resistivity gradientshttps://ui.adsabs.harvard.edu/abs/2015A%26A...574A..10L/abstract
Convective Overstability in Accretion Disks: Three-dimensional Linear Analysis and Nonlinear Saturation
https://ui.adsabs.harvard.edu/abs/2014ApJ...789...77L/abstract
Elliptic and magneto-elliptic instabilities
https://ui.adsabs.harvard.edu/abs/2013EPJWC..4604003L/abstract
A Parameter Study for Baroclinic Vortex Amplification
https://ui.adsabs.harvard.edu/abs/2013ApJ...765..115R/abstract
Rossby Wave Instability at Dead Zone Boundaries in Three-dimensional Resistive Magnetohydrodynamical Global Models of Protoplanetary Disks
https://ui.adsabs.harvard.edu/abs/2012ApJ...756...62L/abstract
On the connection between the magneto-elliptic and magneto-rotational instabilities
https://ui.adsabs.harvard.edu/abs/2012JFM...698..358M/abstract
The baroclinic instability in the context of layered accretion. Self-sustained vortices and their magnetic stability in local compressible unstratified models of protoplanetary disks
https://ui.adsabs.harvard.edu/abs/2011A%26A...527A.138L/abstract
Photoelectric instability
Disentangling Planets from Photoelectric Instability in Gas-rich Optically Thin Dusty Diskshttps://ui.adsabs.harvard.edu/abs/2019ApJ...887....6C/abstract
The Interplay between Radiation Pressure and the Photoelectric Instability in Optically Thin Disks of Gas and Dust
https://ui.adsabs.harvard.edu/abs/2018ApJ...856...41R/abstract
Formation of sharp eccentric rings in debris disks with gas but without planets
https://ui.adsabs.harvard.edu/abs/2013Natur.499..184L/abstract
Planet migration
Orbital Migration of Interacting Low-mass Planets in Evolutionary Radiative Turbulent Modelshttps://ui.adsabs.harvard.edu/abs/2012ApJ...750...34H/abstract
Formation of Planetary Cores at Type I Migration Traps
https://ui.adsabs.harvard.edu/abs/2011ApJ...728L...9S/abstract
Orbital Migration of Low-mass Planets in Evolutionary Radiative Models: Avoiding Catastrophic Infall
https://ui.adsabs.harvard.edu/abs/2010ApJ...715L..68L/abstract
Planetary shocks
On Shocks Driven by High-mass Planets in Radiatively Inefficient Disks. III. Observational Signatures in Thermal Emission and Scattered Lighthttps://ui.adsabs.harvard.edu/abs/2017ApJ...849..164H/abstract
On Shocks Driven by High-mass Planets in Radiatively Inefficient Disks. II. Three-dimensional Global Disk Simulations
https://ui.adsabs.harvard.edu/abs/2016ApJ...817..102L/abstract
On Shocks Driven by High-mass Planets in Radiatively Inefficient Disks. I. Two-dimensional Global Disk Simulations
https://ui.adsabs.harvard.edu/abs/2015ApJ...804...95R/abstract
Code development
Stability Analysis for General Order Central Finite-difference Hyperdiffusivity with Time Integrators of Arbitrary Accuracyhttps://ui.adsabs.harvard.edu/abs/2023RNAAS...7...69L/abstract
Orbital Advection with Magnetohydrodynamics and Vector Potential
https://ui.adsabs.harvard.edu/abs/2017AJ....154..146L/abstract
A Well-posed Kelvin-Helmholtz Instability Test and Comparison
https://ui.adsabs.harvard.edu/abs/2012ApJS..201...18M/abstract
Shallow water
https://ui.adsabs.harvard.edu/abs/2022PSJ.....3..166H/abstract
Ice shell convection
https://ui.adsabs.harvard.edu/abs/2018DPS....5041504C/abstract
https://ui.adsabs.harvard.edu/abs/2017LPICo2048.7021S/abstract
https://ui.adsabs.harvard.edu/abs/2016DPS....4821306U/abstract
MRI
Meridional circulation in turbulent protoplanetary diskshttps://ui.adsabs.harvard.edu/abs/2011A%26A...534A.107F/abstract
Global magnetohydrodynamical models of turbulence in protoplanetary disks. I. A cylindrical potential on a Cartesian grid and transport of solids
https://ui.adsabs.harvard.edu/abs/2008A%26A...479..883L/abstract
Observational
The Alpha Centauri binary system. Atmospheric parameters and element abundanceshttps://ui.adsabs.harvard.edu/abs/2008A%26A...488..653P/abstract
On the difference between nuclear and contraction ages
https://ui.adsabs.harvard.edu/abs/2006A%26A...453..101L/abstract
Fine structure of the chromospheric activity in Solar-type stars - The Hα line
https://ui.adsabs.harvard.edu/abs/2005A%26A...431..329L/abstract
Positional Astronomy
On the Angle of Sunsethttps://ui.adsabs.harvard.edu/abs/2022RNAAS...6..257L/abstract
Educational
A historical method approach to teaching Kepler's 2nd lawhttps://ui.adsabs.harvard.edu/abs/2021AEdJ....1....4L/abstract
Outreach
Ad Astra Academy: Using Space Exploration to Promote Student Learning and Motivation in the City of God, Rio de Janeiro, Brazilhttps://ui.adsabs.harvard.edu/abs/2020CAPJ...27....5L/abstract