 |
 |
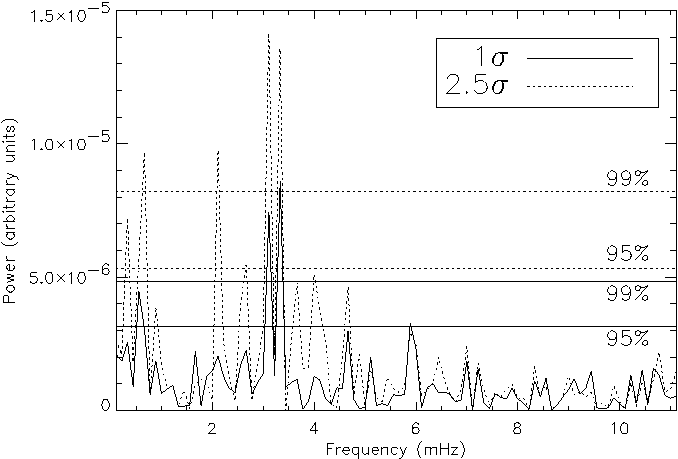
All lightcurves at each threshold for all the NBPs were filtered, subjected to a Fourier analysis and the power spectrum inspected for significant peaks. In Figure 4.6 we show an example of how the power spectrum changes with increasing threshold. At high frequencies, the power spectra are very similar for both thresholds, showing no peaks above 5 mHz. At low frequencies the power spectra are markedly different. The power of the two largest peaks, at 3.11 mHz and 3.33 mHz, has increased by a factor of ~2 when the higher threshold is chosen. Furthermore, a peak at 2.67 mHz has increased by a factor of ~2.5 to over 95% significance, and a peak at 2.11 mHz has increased by a factor of ~5, to well above the 99% significance level.
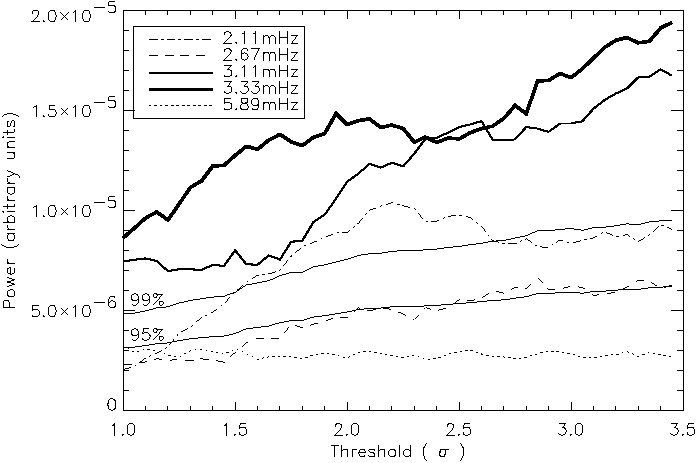
A more detailed graph showing the development of peaks with increasing threshold is given in Figure 4.7. This shows quite clearly the appearance of a 2.11 mHz oscillation at ~1.5σ, peaking in power at ~2.5σ before levelling off around the 99% significance level. The 3.33 mHz and 3.11 mHz frequencies more than double in power from minimum to maximum threshold. A 2.67 mHz frequency also appears, but only to the 95% signficance level, whilst the higher value of 5.89 mHz (although staying at a similar power) becomes less statistically significant. Similar behaviour is repeated in all the other NBPs, but for different frequencies in the 1-4 mHz range. The fact that no single specific frequency dominates throughout the network, combined with the lack of this behaviour in internetwork regions, suggests that this is a real effect.
 |
A summary of the frequencies found in each NBP is shown in Table 4.2. In this table the error is taken to be the frequency resolution (i.e., ±0.11 mHz). There are two distinct types of behaviour described in this table. Some frequencies show a steady increase in power with increasing threshold and, in many cases, are confined to the centre of the NBP. These are denoted `s'. Other frequencies showed a steady increase up to a threshold value, after which there is a plateau in power (or slight decrease). These are denoted as `p'. The `99' and `95' refer to the fact that the power of the frequency reached higher than the 99% and 95% significance levels, respectively. Frequencies at the 95% significance level which only exist for a small range of threshold values are not included, as they may be random effects, although we note the possibility of frequencies only existing in a very small part of a NBP. It also important to note the long duration of our observations means that even the lowest frequencies are trustworthy
| Frequency (mHz) | ||||||||
| NBP | 1.11 | 1.56 | 1.89 | 2.22 | 2.78 | 3.11 | 3.33 | 3.78 |
| 1 | 99 p | 95 s | 99 s | 99 s | ||||
| 2 | 95 p | 95 s | 99 s | 99 s | 99 s | 99 p | ||
| 3 | 95 s | 99 s | 99 s | 95 s | 99 s | |||
| 4 | 95 s | 95 s | 95 p | 99 p | ||||
| 5 | 99 p | 99 p | 99 p | 95 p | ||||
| 6 | 99 p | 95 p | 99 s | 99 p | 95 s | |||
| 7 | 99 p | 99 p | 99 s | |||||
The most striking feature of Table 4.2 is that each NBP exhibits a different oscillatory signal. Some NBPs only show power at the higher (i.e., NBP 1, NBP 4) or lower (i.e., NBP 7) frequencies. Others exhibit strong oscillatory power throughout the entire frequency range (e.g., NBP 5). In terms of frequency occurrence, the 2.22 mHz, 2.78 mHz and 3.33 mHz oscillations are most popular (6 NBPs, with 3.33 mHz always at 99% significance), followed by 1.11 mHz, 3.11 mHz and 3.78 mHz (all in 4 NBPs), 1.56 mHz (2 NBPs) and 1.89 mHz (only 1 NBP). There is no oscillatory power above 4 mHz in any NBP. Concentrating on any one type of behaviour (`s' or `p'), only the 2.78 mHz oscillation is constant. Power at this frequency always seems to steadily increase with increasing threshold.