 |
 |
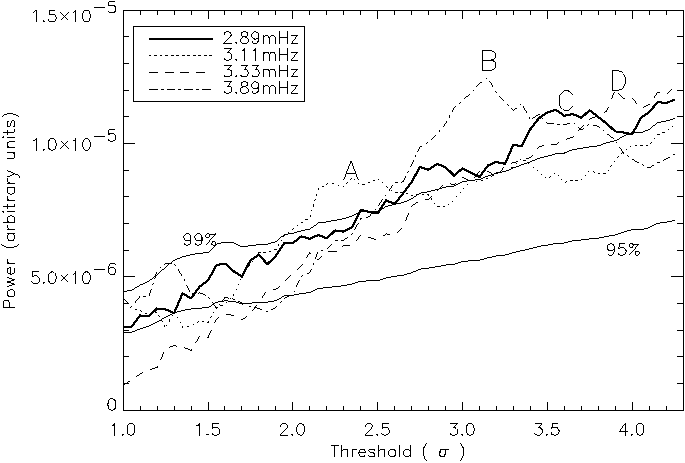
It can clearly be seen from Figure 4.8 that particular frequencies may dominate in different areas of a NBP. At maximum threshold, the 3.33 mHz frequency dominates (point D). With smaller threshold, hence including more of the edge of the NBP, 2.89 mHz (point C), 3.89 mHz (point B) and 3.11 mHz (point A) dominate in turn. As these incremented thresholds refer to a series of nested contours, this highlights how the power spectrum is highly dependent on the chosen threshold value. Hence all frequencies found in the network are spatially localised at both large scale (i.e., the entire network cannot be assumed to have a global mode) and small scale (i.e., even within a NBP different frequencies may dominate in different sections). When the entire 100" X 100" image is used to create lightcurves using a similar method, (i.e., summing over all NBPs) it is the ~2.22 mHz (steadily increases) and ~1.00 mHz (plateaus) frequencies which dominate. This agrees with the results of Lites et al. (1993), who only use one NBP, and Cauzzi et al. (2000) who used the average of eleven.
The 3.33 mHz frequency (5-minute) has been previously reported in solar network regions (Kneer & von Uexküll 1993; Al, Bendlin, & Kneer 1998; Bocchialini et al. 1994; Baudin et al. 1996). However, it does not appear in all the NBPs, and in several cases is not the dominant frequency. Hence it does not appear to be connected to the well known 5-minute oscillation. Instead the results presented here suggest it localised to specific NBPs.
Despite the seemingly random selection of oscillatory power in Table 4.2, a connection to existing theories can be drawn. In most cases, the onset of low-frequency oscillations coincides with the disappearance of higher frequencies (Figure 4.7), suggesting that gravity or magnetism is the dominant restoring force in the centre of NBPs, at the expense of weaker acoustic waves (νac ~5.5 mHz). Lou (1995) suggested that diverging magnetic flux tubes in the chromosphere and lower corona forms a magnetic bottle that can trap magneto-gravity modes. This scenario can create long-period oscillations in the range 1200-200 s (0.8-5.0 mHz) in the chromospheric network. All frequencies found here fall within this range,
Kalkofen (1997) shows how fast-mode MHD waves at frequencies greater than ~1.3 mHz can be excited by granular buffeting (Hasan & Kalkofen 1999). These propagate upward and couple with weaker slow-mode MHD waves at a higher frequency of ~3.4 mHz, thereby transferring power to the slow-mode waves. These longitudinal slow-mode waves become shocks, thereby heating the upper chromosphere. Ulmschneider, Zähringer, & Musielak (1991) show that during coupling a fast-mode wave at frequency ν, will transfer most its energy to a slow-mode wave at frequency 2ν, although some energy will be left in waves at the original frequency ν. This agrees with Table 4.2 where the weaker, less common, lower frequencies may be the signature of the fast-mode waves, and the stronger, more frequent, higher frequencies may be the onset of the slow-mode waves
The tendency of NBPs to exhibit stronger oscillatory power in the centre of NBPs has also been pointed out by Judge et al. (2001). They use the phrase `magnetic shadows' to describe the decrease in both intensity and oscillatory power in the 3-8 mHz range near but not directly above magnetic elements. This is discussed in terms of upwardly propagating acoustic waves reaching the magnetic canopy and undergoing mode-conversion to MHD waves suggesting `magnetic heating occurs only close to the center of expanding flux tubes, not throughout them'.
In this chapter I have presented a contour & contrast method to identify frequency peaks with particular spatial position inside NBPs. Frequencies detected confirm the ~2.2 mHz and ~3.3 mHz values found previously. New frequencies are also detected at 3.78 mHz, 3.11 mHz, 2.78 mHz and 1.11 mHz in several NBPs, whereas 1.56 mHz only occurs in two NBPs and 1.89 mHz only one. The lack of detection of these frequencies in previous studies may be due to the improved method of isolation of each NBP and a higher frequency resolution. The frequencies found agree with the existence of a magnetic component in the waves, either as magneto-gravity waves or magneto-acoustic waves. In the next chapter I will extend this search from one dimension (i.e., distance from NBP centre, r), into 2 extra dimensions (height in solar atmosphere, z, and localised time domain, t) in order to look for waves propagating throughout the chromosphere.