

Next: Heating Theories
Up: Chapter 2
Previous: Magneto-Acoustic-Gravity Waves
Inhomogeneous Plasmas
For a homogeneous plasma, the velocity, vM, of magneto-acoustic wave propagation normal to the magnetic field, is obtained by analogy with Eqn. 26 and Eqn. 29, as,
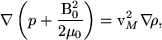 |
(56) |
which reduces to (Narain & Agarwal 1994),
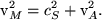 |
(57) |
In general, MHD waves in a homogeneous plasma may be anisotropic, but will always be non-dispersive.
Although MHD waves are extremely complex in the chromosphere (Rosenthal et al. 2002), much progress has been made in the study of thin flux tubes in this region of the atmosphere (e.g., Spruit 1981a; 1981b). This is achieved by assuming magnetic field lines are confined in thin tubes creating an inhomogeneous plasma in which various waves modes may exist. These wave modes are dispersive, which will allow for formation of wave packets and dissipation.
Figure 2.2:
The three modes of waves in a thin flux tube. Left to Right: The sausage (longitudinal) mode, the kink (transverse) mode and the Alfvén (rotational) mode. In each case the magnetic field is directed along the z axis (Narain & Agarwal 1994)
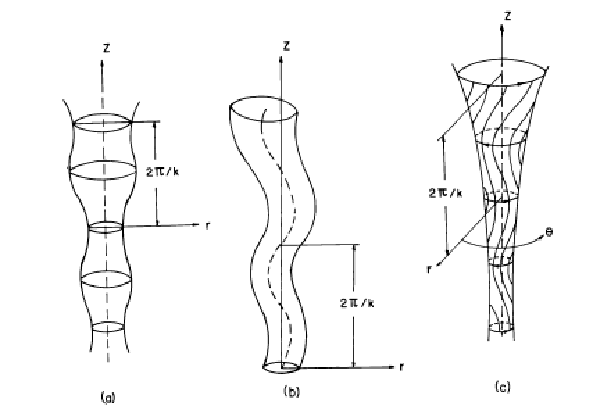 |
The three basic modes for waves in a flux tube are described in Figure 2.2. The sausage-mode wave is a longitudinal wave whereby the tube cross-section expands and contracts due to compressions and rarefactions of the gas. These, acoustic-like, waves propagate along the tube with characteristic speed, cλ, given by (Roberts 2000),
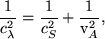 |
(58) |
which can be also be written as (Kalkofen 1997),
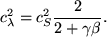 |
(59) |
The kink-mode wave is a transverse wave whereby the field lines in the tube are displaced laterally. It can be thought of as an Alfvén wave which is reduced in speed by the inertia of the tube surroundings. It has a characteristic speed, ck, given by (Roberts 2000),
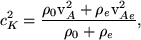 |
(60) |
where subscript e refers to external parameters (i.e., outside the flux tube). For an isolated flux tube such as found under photospheric conditions, 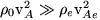 , and Eqn. 60 can be expressed as (Kalkofen 1998),
, and Eqn. 60 can be expressed as (Kalkofen 1998),
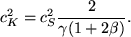 |
(61) |
Both modes follow a dispersion relation similar to Eqn. 37, of the form (Spruit & Roberts 1983),
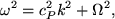 |
(62) |
where cp is the mode's speed of propagation (ck or cλ), and Ω is the mode cut-off frequency. For each mode the wave will be propagating for ω > Ω (i.e. k2 > 0) and evanescent for ω < Ω (i.e. k2 < 0). The cut-off frequencies are given in Kalkofen (1998) as,
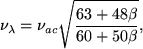 |
(63) |
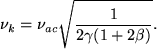 |
(64) |
As in Section 2.3.1, impulsive wave generation will result in a wave front moving at the respective tube speed, with a trailing wake which will oscillate at the respective cut-off frequency. The third mode is the torsional Alfvén wave, which is a rotational oscillation of the tube.
The flux tubes will spread horizontally with height, due to the pressure stratification, so that somewhere in the high chromosphere they fill out to occupy the whole space and create the magnetic canopy. In the canopy the field can once again be thought of as homogeneous, the torsional wave goes over into the Alfvén wave and the sausage and kink waves go over into the slow and fast waves. Furthermore non-linear mode conversion (mode-coupling) is expected to occur in the canopy.


Next: Heating Theories
Up: Chapter 2
Previous: Magneto-Acoustic-Gravity Waves
James McAteer
2004-01-14

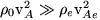 , and Eqn. 60 can be expressed as (Kalkofen 1998),
, and Eqn. 60 can be expressed as (Kalkofen 1998),