

Next: Waves
Up: Fluid Dynamics
Previous: Equation of Energy Conservation
Equation of Momentum Conservation
By Newton's second law the equation of motion may be written as,
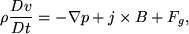 |
(22) |
where Fg is the force due to gravity (viscosity is neglected). Thus, the force per unit volume (LHS) is equal to the summation of forces given by a pressure gradient, a Lorentz force, and gravity. This equation connects the fluid motions to Maxwell's equations via the j X B term. By assuming a gravitational force of the form 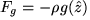 (where
(where 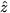 is the outward normal from the solar surface) this becomes,
is the outward normal from the solar surface) this becomes,
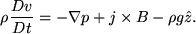 |
(23) |
By simple use of Ampere's law (Eqn. 6) and a vector identity, the Lorentz force in Eqn. 23 reduces to,
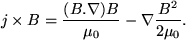 |
(24) |
The first term on the RHS represents a force due to magnetic tension, parallel to B, which results from the curvature of the magnetic field lines. The second term on the RHS is a scalar magnetic pressure force. The plasma β parameter is the ratio of the the plasma pressure to this magnetic pressure and is given by,
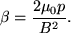 |
(25) |
So for β > 1 pressure dominates, whereas for β < 1 magnetism dominates.
When the plasma flow speed is less than the sound speed, Alfvén speed and free-fall speed, magnetohydrostatic equilibrium exists and the forces in Eqn. 23 balance. In a direction perpendicular to the field lines, n, and substituting for the Lorentz force from Eqn. 24, Eqn. 23 reduces to,
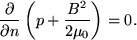 |
(26) |
Define a thin flux tube such that the internal and external pressures are pi and pe respectively, such that the total pressure inside and outside the tube is the same, i.e.,
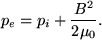 |
(27) |
Hence pi will be less than pe, the internal mass density will also be lower than the external mass density, and (assuming thermal balance) the flux tube will rise. Thus magnetic buoyancy will cause magnetic flux tubes in the convection zone to rise to the surface.


Next: Waves
Up: Fluid Dynamics
Previous: Equation of Energy Conservation
James McAteer
2004-01-14
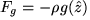 (where
(where 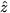 is the outward normal from the solar surface) this becomes,
is the outward normal from the solar surface) this becomes,