

Next: The Induction Equation
Up: Chapter 2
Previous: Outline of this Chapter 2
The set of equations describing the behaviour of the electric field, E, magnetic field, B (actually B is magnetic induction but is commonly referred to as magnetic field in astrophysics), and current density, j, were first combined by Maxwell (1873). These are as follows. Firstly, Poisson's equation,
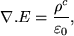 |
(4) |
where ρc is charge density and ε0 is the permittivity of free space. This states that a net charge will act as a source for an electric field. Secondly, Faraday's law,
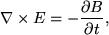 |
(5) |
which states that a change in magnetic field with time will produce an electric field. Thirdly, Ampere's law,
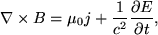 |
(6) |
which states that either a current, or time-varying electric field will produce a magnetic field. In this equation μ0 is the magnetic permeability of free space, related to the speed of light, c, by,
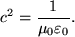 |
(8) |
Under the MHD approximation, whereby plasma velocities, v, are much less than the speed of light, the second term on the RHS of Eqn. 6 is ignored. Finally, Gauss' law,
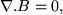 |
(8) |
such that there are no magnetic monopoles. In addition to the four Maxwell's equations above, Ohm's law states that, in a frame of reference moving with the plasma, the current density is proportional to the sum of the electric field due to the movement of the plasma (v X B) plus the electric field which would act on it at rest, E, i.e.,
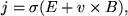 |
(9) |
where σ is electrical conductivity.
Subsections


Next: The Induction Equation
Up: Chapter 2
Previous: Outline of this Chapter 2
James McAteer
2004-01-14