

Next: Fluid Dynamics
Up: Maxwell's Equations
Previous: Maxwell's Equations
The electric field can be eliminated between Faraday's law and Ohm's law to give,
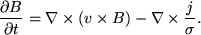 |
(10) |
This reduces, by Ampere's law, to,
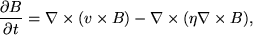 |
(11) |
where 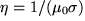 is magnetic diffusivity. By simple use of a vector identity, using Gauss's law, and assuming constant 1 η this further reduces to,
is magnetic diffusivity. By simple use of a vector identity, using Gauss's law, and assuming constant 1 η this further reduces to,
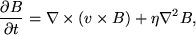 |
(12) |
which is known as the induction equation. This states that a local change in the magnetic field is due to both convection and diffusion. The magnetic Reynolds number is the ratio of the convective to the diffusive term,
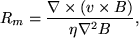 |
(14) |
and is an indication of the coupling between the plasma flow and the magnetic field. This can simply be approximated to,
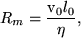 |
(14) |
for length scale, l0, and plasma speed, v0
For large Rm (»1), as found in most astrophysical cases, the convective term dominates in Eqn. 12, and the field lines move as if they are frozen into the plasma (Alfvén, 1943) with typical timescale, tc = l0/v0. For small Rm («1), typically found in laboratory plasmas, the diffusion term dominates and flux `leaks' with typical ohmic diffusion timescales then given by td = l02/η. For typical solar photospheric values (v0 10 m s-1,η~ 103 m2 s-1) Rm becomes less than unity (td ~ tc) for l0 ~ 100m, ohmic dissipation becomes important, and magnetic reconnection may occur.
1 In fact η varies with both temperature and density, from ~ 103 m2 s-1 in the photosphere to ~ 1 m2 s-1 in the corona (Priest 1982)


Next: Fluid Dynamics
Up: Maxwell's Equations
Previous: Maxwell's Equations
James McAteer
2004-01-14
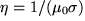 is magnetic diffusivity. By simple use of a vector identity, using Gauss's law, and assuming constant 1 η this further reduces to,
is magnetic diffusivity. By simple use of a vector identity, using Gauss's law, and assuming constant 1 η this further reduces to,
![]()
![]()
![]()