Heating Theories

The most important factors in any heating theory involving waves are initially creating a wave and then transferring the energy to the upper chromosphere where the energy has to be deposited. These factors are generally discussed as follows.

• Generation - Flux tube waves can be generated at the photosphere in a number of ways: transverse buffeting by granules can create kink waves; pressure changes can create sausage waves; twists in the tube may create torsional waves.

• Propagation - Only oscillations with frequencies above the respective cut-off will propagate, otherwise waves will be evanescent.

• Dissipation - When waves reach the required height in the atmosphere the mechanical energy has to be transferred to heat energy in the surrounding plasma. This can be achieved in a variety of ways, the most common of which is by the wave shocking.

Figure 2.3: A sinusoidal wave changes shape with increasing height in a stratified atmosphere. As the compressed regions travel faster, a wave shock front is gradually formed. (Bird 1964)

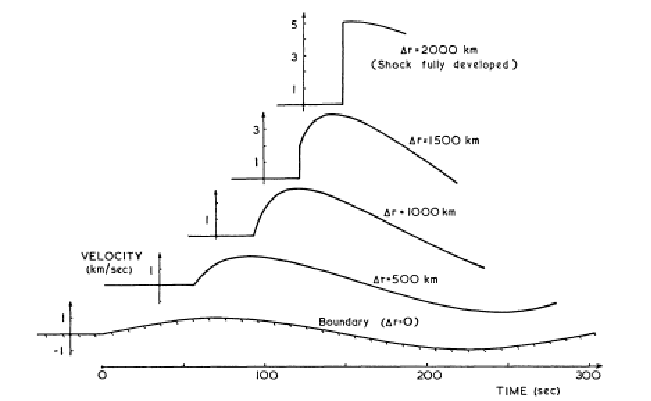
For longitudinal modes, the waves cannot directly heat the surrounding gas, instead they cause the plasma to vibrate. As they move up through the atmosphere ρ decreases and the wave amplitude, V, increases so the total wave energy, ρV², remains constant. In effect, the sinusoidal form of the original wave is distorted such that compressed regions travel faster than rarefied regions. Eventually, when the amplitude reaches the sound velocity a shock front is formed (Figure 2.3). The rise in both density and temperature behind the shock wave increases the rate of radiation, hence creating an important dissipation mechanism. This form of heating is found to be efficient in the lower chromosphere for acoustic waves (Phillips 1992). In the presence of a magnetic field shocks are much more complicated but, similar to acoustic waves, MHD waves in general shock when any disturbance within the wave moves faster than the characteristic wave speed. In recent years further theories (e.g., phase mixing, resonant absorbtion) have also been proposed as possible heating mechanisms.

Throughout Chapters 4 - 6 I discuss various AC chromospheric heating theories based on the equations and wave modes described above. The generation, propagation and dissipation of different wave modes lead to different oscillations. The search for these oscillations gives an indication of which wave mode, and hence which heating mechanism, may be present in different parts of the chromosphere. The observations used to search for these oscillations are described in the next chapter.