

Next: Acoustic, Gravity, & Acoustic-Gravity
Up: Waves
Previous: Waves
Acoustic Velocity & the Klein Gordon Equation
Initially I will neglect the magnetic field, and concentrate on the effects of sound waves in a stratified atmosphere (i.e., set B=0). Assume a simple adiabatic expansion of the form,
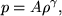 |
(28) |
where A is a constant. Taking the gradient of both sides of this equation leads to,
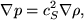 |
(29) |
where the acoustic velocity, cs is given by,
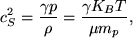 |
(30) |
where KB is the Boltzmann constant, μ is the mean molecular weight, and mp is the proton mass. Hence cs ∝T0.5 and varies from around 9 km s-1 in the photosphere to over 200 km s-1 in the corona.
Under hydrostatic equilibrium conditions, Eqn. 23 becomes,
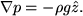 |
(31) |
Using the ideal gas equation, and for an isothermal medium stratified in the z axis, this can simply be integrated to obtain (Roberts 2003),
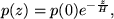 |
(32) |
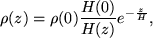 |
(33) |
where H is the pressure scale height,
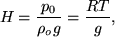 |
(34) |
typically around 150 km in the photosphere. Hence pressure and density both fall off exponentially with height. Furthermore, by considering small temporal perturbations in the z axis, it can be shown that acoustic type waves will obey the Klein Gordon equation (Lamb 1909; Roberts 2003) whereby,
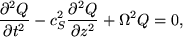 |
(35) |
where Ω has frequency dimensions, and the initial perturbation, u, is directly proportional to the new term, Q, such that |u| ∝ p-0.5|Q|. Hence a typical photospheric velocity of around 1 km/s will rapidly increase to a value approaching the sound speed within 600 km (4 scale heights approximates to a 2e increase), leading to the possibility of damping mechanisms (e.g., wave shocks (Section 2.5)).
The Ω term in the Klein Gordon equation (35) introduces a timescale onto the perturbations. Assume a solution to Eqn. 35 of the form,
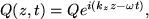 |
(36) |
where ω is the angular frequency (=2πν) and kz is the wavenumber (=2π/λ). Hence 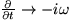 and
and 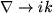 in Eqn. 35, which becomes,
in Eqn. 35, which becomes,
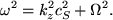 |
(37) |
From Eqn. 37, it is clear that real solutions only exist for values of ω greater than Ω, otherwise waves are evanescent (i.e., 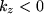 ). This acoustic cut-off frequency is defined as,
). This acoustic cut-off frequency is defined as,
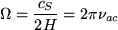 |
(38) |
which leads to νac ~ 5 mHz around temperature minimum.
The increased temperature in the solar interior forms a refractive boundary for acoustic waves. A second boundary is formed at the photosphere due to a sharp density gradient. Waves with a frequency above the acoustic cutoff can escape the photospheric boundary, otherwise they will be reflected back toward the resonant cavity and form a standing wave (and studied as p-modes in helioseismology).
It can be shown (e.g., Lamb 1932; Erdélyi 1954) that the impulsive generation of a wave will lead to a wavefront propagating with velocity cs. Ahead of this wavefront the medium will be at rest, but the trailing wake of the wavefront will be oscillating at the characteristic frequency, Ω. In addition the amplitude of this oscillation will decay in time as the wavefront moves through the medium. This is directly analogy with the inhomogeneous case (Section 2.4).


Next: Acoustic, Gravity, & Acoustic-Gravity
Up: Waves
Previous: Waves
James McAteer
2004-01-14
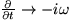 and
and 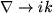 in Eqn. 35, which becomes,
in Eqn. 35, which becomes,
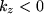 ). This acoustic cut-off frequency is defined as,
). This acoustic cut-off frequency is defined as,