

Next: Magneto-Gravity Waves
Up: Magnetic Waves
Previous: Alfvén Waves
By taking the scale product of Eqn. 49 with k and B0 in turn leads to a pair of equations which combine to give,
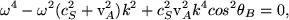 |
(54) |
and (for k.v1 = 0) the Alfvén wave of Eqn. 53. As Eqn. 54 is quadratic in (ω2/k2) the solutions are simply,
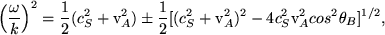 |
(55) |
yielding two outwardly propagating waves termed the fast-mode and the slow-mode (defined by their phase velocity) in addition to the Alfvén wave. The characteristics of each type of wave in a strong and weak magnetic field are summarised in Table 2.1. Essentially, the fast- and slow-mode waves may be regarded as a sound wave modified by the magnetic field, and an Alfvén wave modified by the pressure. In the limits of B = 0 or ρ = 0, the fast-mode becomes a sound wave or Alfvén wave respectively and the slow-mode vanishes.
Table 2.1:
Summary of magneto-acoustic modes. Direction of propagation, and dominant restoring force and velocity of waves with strong and weak magnetic fields are given. (after Stein & Leibacher 1974)
| Mode of Wave |
Propagation Direction |
Magnetic Field |
| Strong |
Weak |
| Alfvén |
along B |
Magnetic Tension, vA |
| |
|
|
|
| Fast |
Isotropic |
Magnetic Pressure |
Gas Pressure |
| |
|
~vA |
~cS |
| Slow |
approximately |
Gas Pressure |
Magnetic Tension |
| |
along B |
~cS |
~vA |


Next: Magneto-Gravity Waves
Up: Magnetic Waves
Previous: Alfvén Waves
James McAteer
2004-01-14