

Next: Magneto-Acoustic Waves
Up: Magnetic Waves
Previous: Magnetic Waves
As discussed in Section 2.2.3 the Lorentz force can be interpreted as the sum of a magnetic tension (B2/μ0) and a magnetic pressure (B2/2μ0). By analogy with a string under tension, this will permit transverse waves with an Alfvén velocity, vA, given by,
 |
(50) |
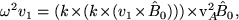 |
(51) |
which can be reduced by vector identity to,
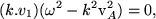 |
(52) |
which has two distinct solutions. For k.v1 = 0, Eqn. 51 (after multiplying out the vector products) becomes
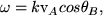 |
(53) |
where θB is the angle between k and B0. This is the shear Alfvén wave, with a phase velocity which is just the Alfvén velocity along the magnetic field and zero perpendicular to it, and a group velocity which is always directed along the magnetic field. The k.v1 = 0 property means that the velocity is perpendicular to the direction of propagation, hence the waves are transverse. The second solution, ω =kvA, is the compressional Alfvén wave, which propagates isotropically.


Next: Magneto-Acoustic Waves
Up: Magnetic Waves
Previous: Magnetic Waves
James McAteer
2004-01-14