

Next: Filtering
Up: Data Analysis
Previous: Contrast Lightcurves
Fourier Analysis
A Fourier analysis was carried on each lightcurve using routines written in SSWIDL. For a continuous signal, f(t), sampled at N discrete values, fk (k=0, 1, 2, ...., N-1), the discrete Fourier transform (DFT), Fj (j=N/2, N/2-1, ..., -N/2+1) is given by,
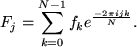 |
(67) |
Each sample is separated by a time interval, δt, such that the entire signal lasts for time T=δt x (N-1). Each value of Fj corresponds to the Fourier transform at a frequency νj = j/Nδt, hence the maximum detectable frequency, termed the Nyquist frequency is given by,
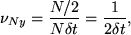 |
(68) |
and the frequency resolution, is given by,
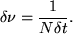 |
(69) |
A poor frequency resolution will blend peaks in the Fourier spectrum, and the Fourier analysis will be susceptible to the picket fence effect (Section 4.2.4).
Where the DFT will be complex and of the form a(j)+ib(j), the Fourier amplitude, Aj, phase, Φj, and power, Pj, can be determined from,
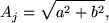 |
(70) |
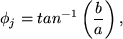 |
(71) |
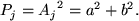 |
(72) |
A useful check at this stage is to ensure the resulting Power spectrum obeys Parseval's theorem, whereby the total Fourier power should be equal to the variance of the original signal, i.e.,
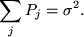 |
(73) |
A study of the statistical significance of peaks in the power spectrum can be made by assuming a Gaussian distribution for each point in the signal. Hence each point in the power spectrum will have a χ2 distribution, with two degrees of freedom (DOF). For a significance level, sig, (where 0 < sig < 1), the corresponding value for the power spectrum, Psig, will be
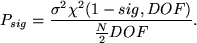 |
(74) |
This equation is used throughout at both the 99% (sig = 0.99, χ2(0.01,2) = 9.21) and 95% (sig = 0.95, χ2(0.05,2) = 5.99) level. Essentially this means that if one hundred Fourier peaks were chosen at random, five would have power above the 95% level, and one would have power above the 99% level.


Next: Filtering
Up: Data Analysis
Previous: Contrast Lightcurves
James McAteer
2004-01-14