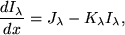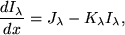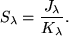

Next: Chromospheric Lines
Up: The Fraunhofer Lines
Previous: The Fraunhofer Lines
Photospheric Lines
By the equation of radiative transfer,
the change in intensity, I, at any wavelength, λ, over a distance, x, is dependant on two processes, absorption and emission. The absorption coefficient, Kλ is essentially the fraction of energy removed from a beam, either by absorption or scattering, per unit length. The emission coefficient, Jλ, is a measure of the amount of energy added to the beam. The source function, Sλ, is then the ratio of emission to absorption,
In an ideal situation, where the atoms and photons of a gas are completely interacting, the Sun can be equated to a black body and hence the source function can be equated to the Planck function. However for the Sun, where some radiation escapes, this can only be achieved through the local thermodynamic equilibrium (LTE) approximation. Here the source function is approximated to the Planck function at the local temperature value. This is equivalent to the `grey atmosphere' approximation where the absorption coefficient is independent of wavelength. The departure of the solar continuum curve from that of a black body (Figure 1.2) is due to the fact that the absorption coefficient is dependent on wavelength. For larger absorption coefficients, radiation is emitted from higher in the atmosphere, where the temperature is cooler (i.e., as far up as the temperature minimum). This applies to the wavelengths of the Fraunhofer lines. Conversely for other parts of the spectrum, radiation comes from lower in the atmosphere where the temperature is hotter. As a result of this temperature difference the total flux emitted from the Sun in the Fraunhofer lines is lower than the continuum, hence the lines appear dark.


Next: Chromospheric Lines
Up: The Fraunhofer Lines
Previous: The Fraunhofer Lines
James McAteer
2004-01-14