Lab 1: Density and Gravity
Key Definitions.
- Weight - How much a planet/moon/etc. pulls down on an object. This is larger for more massive objects, more massive planets, or planets that are smaller in size.
- Mass - How much "stuff" is in the object. (Specifically, the number of protons and neutrons.) This is a property of the object itself, and is not affected like the object's location.
- Volume - How much space an object takes up. This also depends only on the object itself.
- Density - Mass divided by volume, or how compact the object's mass is. This depends on the material(s) the object is made of, but it does not matter how much of that material you have.
In planetary science, we tend to lump the different types of solid* material we most commonly encounter into three large categories. Here they are from least dense to most dense:
- Ice. Could be frozen water, or frozen CO2 ("dry ice"), frozen nitrogen, or any frozen material that is usually a liquid or gas here on Earth.
- Rock. Usually this consists of silicate materials.
- Metal. The most common metals around are iron and nickel.
*Liquids are rarely encountered in the solar system, and gases are too easily compressible to get "true-almost-everywhere" density values.
Does larger mass mean larger density?
- Not necessarily. Consider an ice cube, a gold brick, and a boulder. Clearly, the boulder is the most massive, and the ice cube is the least massive. However, if we calculated the density of each object, we'd probably get something along the lines of...
- Ice cube: 0.93 g/cm3
- Gold brick: 19.3 g/cm3
- Big boulder: 2.7 g/cm3
The gold brick is more dense than the boulder, because gold is denser than rock, even if it's a little bit of gold versus a lot of rock. This is because density is also affected by the volume. If we had two objects, A and B, that had the same volume, but A was more massive, then A would also be denser. If A were more massive but smaller in size, it would be denser. However, if A is more massive and larger in size, then we'd have to do the math to figure out which object is denser.
More Key Definitions.
- A meteor is a random piece of space debris (usually from a comet or asteroid) that flies through the Earth's (or another planet's) atmosphere, attracted by the gravitational pull.
- A meteorite is a meteor that actually hits the ground. This is also used to refer to the fragment of the original object that is still around afterwards (if there is one).
- A crater is the bowl-shaped hole that is caused by a meteorite impact.
- Things from space that crash into larger bodies (like planets and moons) are also sometimes called impactors.
Linear Fitting-
We know that the faster an object is travelling when it hits, the larger the crater it makes. But can we figure out more details on how they are related? Science goals in situations like this are to develop formulas that can say, "If you tell me how fast this object is falling to the ground, I can tell you how big a crater it'll make." This is where linear fitting comes in. We plot this versus that, for various thisses and thats, looking for a plot where the points are in a line.
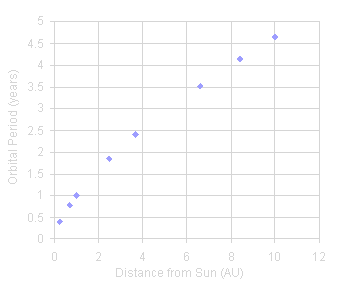
In this case, if you draw a line from the leftmost points and extend it, the rest of the points fall below the line. This says that the y-axis values (orbital period, here) increase relative the the x-axis values (distance from Sun) at a slower-than-linear rate. The y-values do not increase as quickly as the x-values do.
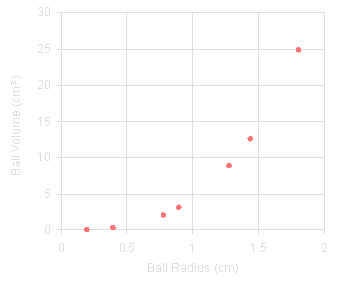
Here, if we draw a line connecting the two leftmost points, the rest of the data points will be above the line. In this case, the y-values are increasing too quickly for a linear rate. Thus we have a faster-than-linear rate.
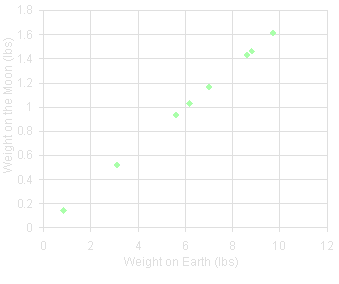
Lastly, in this plot we see that the data points all fall more-or-less right on the same line. If we draw a line connecting the two leftmost points and extend it to the right, the other points will not tend to drift away from this line. What we have here is a linear rate. This is good, because now we can relate the two different values with a simple equation:
y = k x x
...where k is some constant value that we get from the angle of the line. Here, if we figure the values out, we can say that an object's Moon weight (in pounds) is equal to 1/6 times its Earth weight.
So this is what we're trying to do with the crater sizes in this lab. What values best form a linear fit with the object's speed at impact?
...and as a final thought question, we've seen that the faster an object is falling, the larger the crater it makes. What factors might influence the speed of such impactors? Or to put it another way, if we see two planetary surfaces that get hit by the same sizes of impactors, what might cause one to have larger craters (on average) than the other?
Back to the main page.


