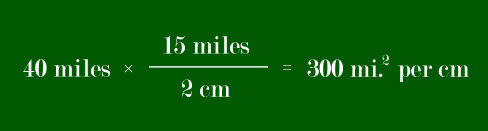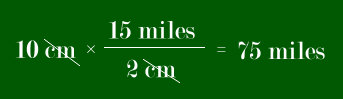Lab 2: Scale Model of the Solar System
In this lab, we have been scaling down values from the real world
to make an accurate model that's easier to view. In order to calculate
the planets' scaled-down distances and diameters, we follow the same
sort of math used when calculating distances on a map.
If you have trouble remembering which numbers to stick where,
it often helps to try a simpler situation in your head, then
backtrack to figure out how you solved it.
For example, let's say you had a map with the scale "3 inches
= 5 miles." How far would a 10-mile distance be on the map?
Yes, six inches. How did we get to that answer? We started
with the distance we knew, divided by the 5 miles, and multiplied
by the 3 inches.
It is easier to see what is going on if we look at it as an
equation. Here, we'll try to figure out how far 40 miles would
be on a map with the scale "2 cm = 15 miles." Doing the same thing
as above, we get

To better understand why we put the map scale as that kind of
fraction, let's do what we always do when multiplying fractions.
Whenever something appears on both the top and the bottom, the two
cancel out. Here, we want to get rid of the "miles" but keep the
centimeters. (Remember, if something is multiplied in and not part of
a fraction, you can picture it as being over 1.)

We can also use this unit-canceling to double-check to make sure
we used the map scale in the right form. If we accidentally put the
map-scale fraction upside-down, then none of the units cancel, and
they all pile up at our answer... leaving us with a value that
doesn't really mean anything:
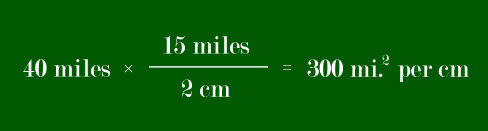
And if we instead wish to go from map distances to real-world
distances, we flip the scale fraction over so that the map units cancel
out. Here we figure out how far 10 cm on the same map will be in the
Real World:
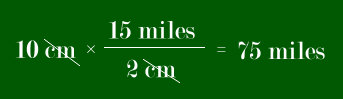
Back to the Scale Model lab.
Back to the main page.