We learned that the HR diagram is a useful tool in examining the lives of stars. Before a star can be called a star (when it first fuses hydrogen in its core), we can track the collapsing cloud through various stages until the star is born on the main sequence. We can also use the HR diagram to track the star as it begins to run out of fuel, as it "dies". The process that governs each stage of a star's life, as well as how long it spends time in each of these stages depends on its mass. All stars spend the vast majority of their lives on the main sequence--the processes of birth and death are short-lived. We found that the Sun spends about 10 billion years on the main sequence. How about other stars? Stars less massive than the Sun (K and M stars) spend much more time on the main sequence--75 billion years (or more)! While stars more massive than the Sun have much shorter lives--only a million years (or less) for very massive stars.
Why is this? In our table giving data on the spectral types of stars (see the notes for class #17) we listed the masses and luminosities of various kinds of stars. The Sun has one solar mass, and one solar luminosity. An "O" star, however, has a mass of 60 solar masses, and a luminosity of 1,400,000 solar luminosities! Note that an O star has 60X the amount of hydrogen that the Sun has--thus it has 60X the amount of available fuel. But note that it is using it up much more quickly: 1,400,000X the rate of the Sun. We can estimate how long this star will live by comparing it to the Sun. If it has 60X the mass, but burns it 1,400,000X faster, the "O" star will only live for 60/1,400,000X as long as the Sun. If you work this out, 60/1,400,000 = 4.3 X 10-5. Multiply this by 10 billion years, and you get: 428,000 years! An O star has a very short main sequence life.
We can do the same thing for an M-type star. Note that they start their main sequence lives with 0.3X the mass of the Sun, so they have about 1/3 the fuel the Sun has. But note that they also have a much lower luminosity: 0.04X that of the Sun. We can divide these numbers: 0.3/0.04 = 7.5 , thus an M star lives 7.5 times as long as the Sun, or 75 billion years. We can think of M stars as like a "Smart Car", they are small, but get good gas mileage, while O stars are like Escalades--a large, gas-guzzling SUV. It is big, and burns a lot of fuel. Why does this happen? The answer, of course, is gravitational pressure. The pressure at the core is larger in high mass stars, this means the temperatures are higher, and the core of the star is larger---the region fusing hydrogen is much larger, and a larger fusing area means that there is more energy output. The opposite occurs in the lowest mass stars--the pressure in their cores is just barely high enough to sustain nuclear fusion in the first place, so the fusion region is tiny, and its energy production is anemic. In fact, we talk about a "Mass-Luminosity" relationship: L ∝ Ma. For real stars, the exponent "a" changes with mass (go here for more on this relationship).
We have discussed the life history of a low mass star--most of the events outlined in that discussion are true for high mass stars also--there are various points in a massive star's life where it runs out of fuel, and at these times, interesting changes occur. Massive stars form in the same way as low mass stars--they just form more quickly because there is more mass to speed-up the process. Whereas the Sun took about 50 million years to contract from a cold gas cloud to a main sequence star, a star with 15 solar masses collapses to the main sequence in 60,000 years. Everything about massive stars is bigger, faster, and flashier! They are the movie stars and billionaires of the astronomical universe.
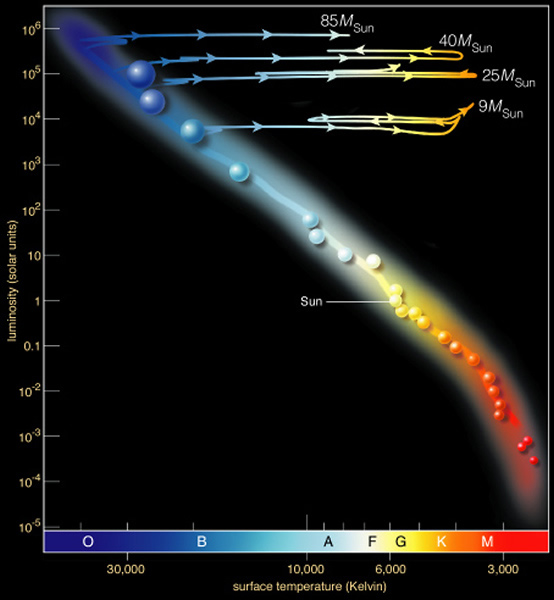
High mass stars generate energy by fusing hydrogen into helium, but use a slightly different technique that involves carbon, nitrogen and oxygen as "catalysts". We will not go into it further (but see figure 17.10). Just like low mass stars, high mass stars eventually run out of fuel at their cores. Gravity then takes over and shrinks the core. The pressure and temperature go up in the core, and simultaneously, a shell of hydrogen burning is formed, as well as a core that is fusing helium into carbon. The energy generation rate is now higher, and the star expands into a red supergiant. The evolutionary track can be plotted in an HR diagram:

This story is similar to that of a low mass star, just that the energy generation rate is higher, and the lifetime is shorter. In the diagram above, you see that the highest mass star (the 85 Msun one) actually never makes it to a red supergiant. We will discuss why in a moment. As the core of the red supergiant uses up the helium and hydrogen, it is forming a core that is rich in carbon. Once the supply of helium and hydrogen is exhausted, the pressure in the core intesifies again. The first big change occurs when the temperature reaches 600 million K. At this point it is now possible to fuse carbon and oxygen into heavier elements:
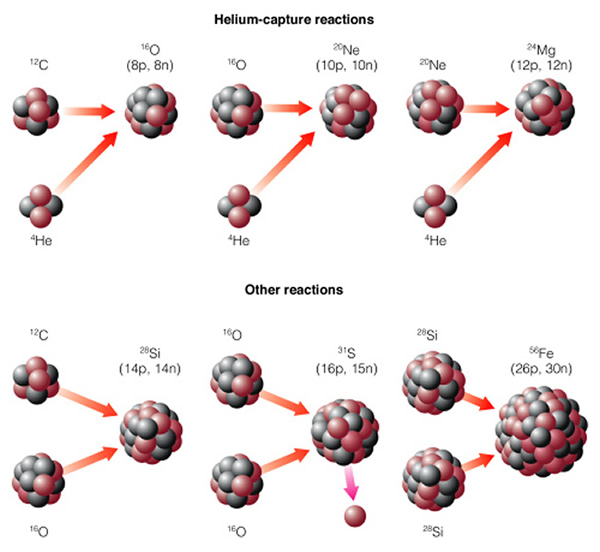
The pace of evolution is accelerating. While the hydrogen and helium burning supergiant phase might last a 100,000 years, the carbon burning phase lasts about 100 years! Each time a fuel source is exhausted, a new type of fusion begins once the pressures and temperatures are high enough to start it. The core of a high mass star is like an onion---a large number of layers where different elements are being fused into heavier elements:
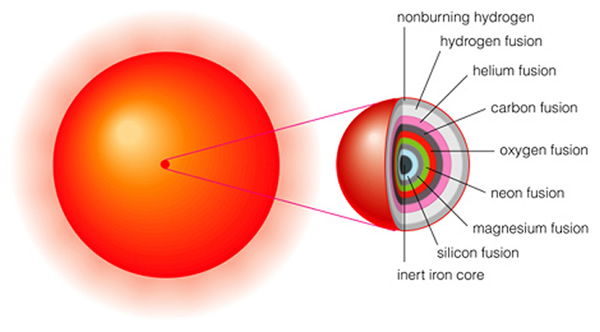
Surprisingly, the outer parts of the star (i.e., the red supergiant photosphere) do not pay too much attention to all of these changes. If the energy generation rate goes up, the star expands a little bit. If the rate goes down, it contracts a little bit. The luminosity stays fairly well fixed, though the star does exhibit "loops" in the HR diagram due to the expanding and shrinking (remember shrinking = hotter => bluer, expanding = cooler => redder). At the very center of the core at the late stages of a massive star's life, silicon is being fused to form iron. Iron is the heaviest element that can be created through a fusion process in which energy is released, as is shown in (a similar figure) Figure 17.14:
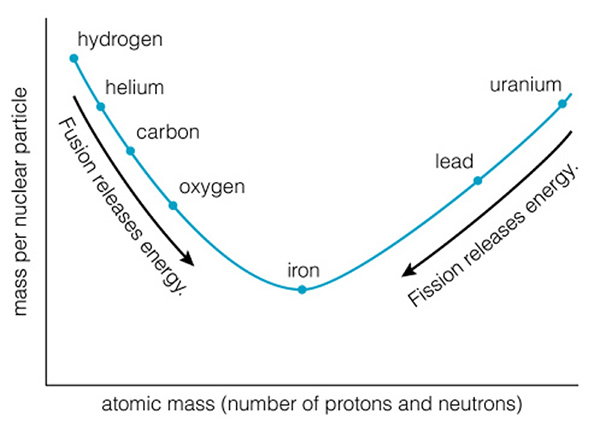
You can fuse iron with other elements to create lead or uranium, but this absorbs energy instead of releasing it. Iron is the end of the road! As the iron core grows in size, and the fuel around it is used-up, the pressure on the core builds. The core begins a dramatic shriking to form a very large "white dwarf" as was done in a low mass star--but now the gravity is strong enough to overwhelm the electron degeneracy pressure (the pressure that results because electrons don't want to sit on top of each other). The electrons are now squeezed so hard that they merge with protons and the proton changes into a neutron (the postive and negative charges cancel, and a neutrino is emitted to balance things):
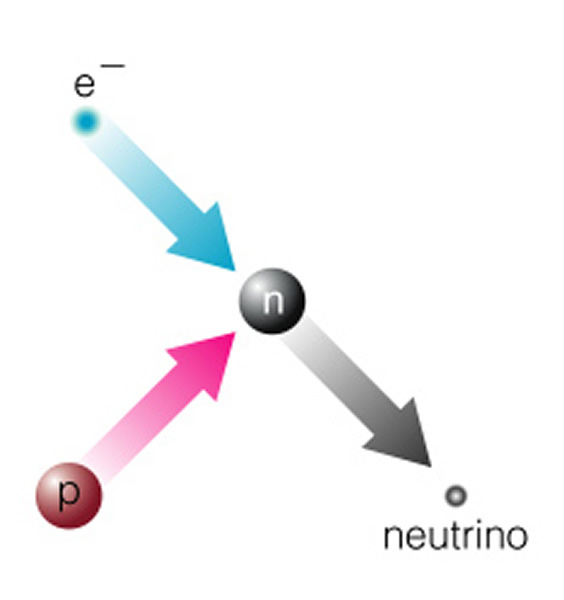
Once this happens, the core instantly (this process takes a fraction of a second to occur) collapses from about few dozen times the diameter of the Earth, down to a sphere of neutrons that is only few kilometers in diameter! Note that this iron core before the collapse begins has a mass of about 2X that of the Sun. The collapse stops because neutrons---like electrons--have their own "degeneracy pressure". Two neutrons cannot occupy the same space--there is only room for one neutron inside the volume of a neutron (just like you cannot fit a thirteenth egg in to a carton that holds one dozen eggs). So, we get a sphere of neutrons about 8 km in diameter--this object has the density of an atomic nucleus--a density of 1016 gm/cm3!!! The end product is something we call a "neutron star", as that is all it is made of.
This rapid collapse produces a neutron star, but it also produces something else: a supernova. The rapid collapse from an object many times the size of the Earth, to something similar in size to Las Cruces, releases an enormous amount of gravitational energy. In fact, the energy generated in this collapse is equivalent to the energy output of 100 suns over their entire 10 billion year lifetimes! This enormous energy production at the core of the star causes an explosion that rips the star apart. The energy blasts its way out into space, and a star that was already 1,000,000 times more luminous than the Sun, becomes ten billion times as luminous as the Sun. In a matter of hours, a normal red giant explodes into a supernova:

Before it blew-up (right hand side), the star is very faint. But afterwards (left hand side), the star is enormously brighter. The supernova causes the outer atmosphere of the supergiant to be torn away, and to expand into space. This hot cloud of glowing gas is called a "supernova remnant". The "Crab Nebula", shown below, is the expanding cloud of gas that resulted from a supernova that occurred in the constellation Taurus in 1054 AD (it was discovered and observed by Chinese astronomers of the time):

Down at the very center of the Crab Nebula is a tiny neutron star that has a temperature of 1 million degrees! Even 1,000 years later, this object remains hot from the collapse of the core of the supergiant star. Supernova are important objects to astronomers because they are so bright we can see them just about right to the edge of the Universe. We will talk about their uses in mapping the structure of the Universe soon.
Earlier, we presented an HR diagram on which the most massive star, that with 85X the mass of the Sun, did not become a red supergiant. Why did it not do this? The reason is that the core is so massive, that it begins collapsing soon after it runs out of hydrogen, and because the core is so massive, it goes through all of the various fusion cycles so quickly that the outer atmosphere does not have time to expand very much before it becomes a supernova. Thus, the most massive stars explode as supernovae before they reach the red supergiant phase.
So far, we have seen two types of degeneracy pressure (electron and neutron) that can stop the collapse of the core of a star. In low mass stars like the Sun, the electron degeneracy pressure halts the collapse of the core, and forms a white dwarf. In massive stars, the collapse of the iron core can be halted by neutron degeneracy pressure. What happens if we have more mass and pressure than neutron degeneracy pressure can resist? Now things really get bizzare. Neutron pressure is the last available source to balance gravity--if gravity is so strong that this pressure is overwhelmed, there is nothing to stop the collapse of the core of a massive star.
What does this mean? It means, in fact, that the core of the star will collapse forever! This object, a core that is collapsing forever, is called a black hole. Black holes have some interesting properties. For example, their gravity is so strong that light cannot escape. Matter that gets too close to a black hole can fall into it, and disappear. Because we cannot see into a black hole (no light), there is no information transferred between the inside of a black hole, and the outside universe. Black holes are considered holes in our Universe---a small region of our Universe from which no information can be gathered, and which material from our Universe can disappear.

The rings of light around the blackhole are due to its gravity bending light, as shown in this animation:

Every object with mass in our Universe "warps" space-time. That is, the X, Y, and Z coordinates of space, and the time axis "T". This four dimensional space that you and I live in is sort of like a rubber sheet in two dimensions. Small objects like the Earth do not really affect it (though the GPS satellites have to worry about Earth warping local space-time!). But more massive objects really disturb space-time, and light can be forced to travel on something besides a straight line:
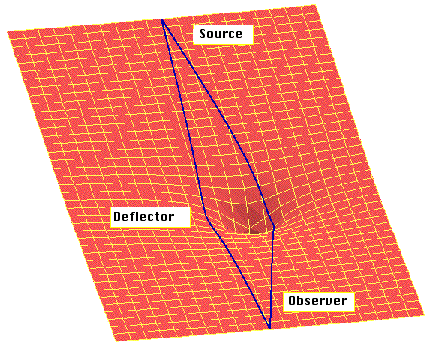
Both space and time are strongly warped by a black hole--in fact time sort-of "stops" at the event horizon--at least for someone falling into a black hole.
Do black holes exist? Yes! You might ask how we can see something that emits no light--we cannot. At least, we cannot see them directly. We can, however, detect their influence on nearby stars. Black holes still have gravity because they still have mass. Thus, objects (such as planets or stars) can orbit a black hole just like objects orbit normal stars. In the process, the black hole can remove matter from this star, and this matter spirals into the black hole. Before it gets there, however, it gets hot, and emits x-rays. We can detect these x-rays, and that is how we know they exist. Here is an artist's conception of one of these systems (Cygnus X-1, the first, and brightest X-ray source discovered in the constellation Cygnus):

The black hole rips matter from the companion star, and this matter spirals into the black hole (central black dot) and emits x-rays. We will talk a bit more about white dwarfs, neutron stars, and black holes in the next class. How "big" are black holes? They are quite small. The relevant radius in discussing a black hole is something called the "event horizon". This is the radius inside of which no information can escape (or any particle, whether matter, or even light!). The equation for figuring out the size of the event horizon is:
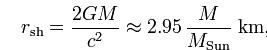
A solar mass black hole would have a radius of 3 km---even smaller than a neutron star. Even though it seems kind of strange, a spinning black hole can be "felt". There is a region around the black hole called the "ergosphere":
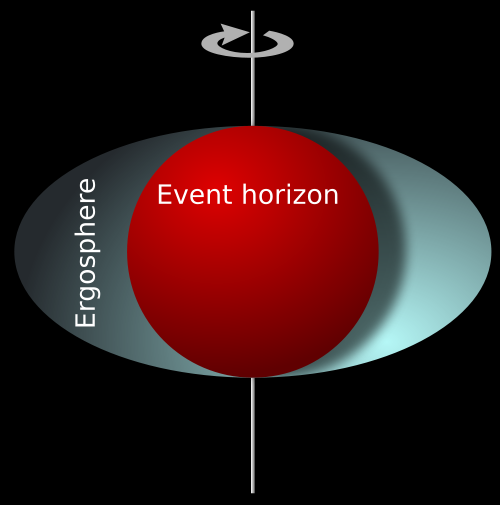
Any object inside the ergosphere will be forced to move in the same direction of rotation as the black hole---this is due to a relativstic process called "frame dragging", and has now been tentatively measured for several rapidly spinning black holes.
So, as we have just found out, stars produce elements through fusion. Low mass stars like the Sun turn hydrogen in to helium, and helium into carbon (and a tiny bit of oxygen). More massive stars produce all of the rest of the elements in the periodic table:

But this process, called nucleosynthesis, is slow, and most of the material we see around us is still hydrogen:
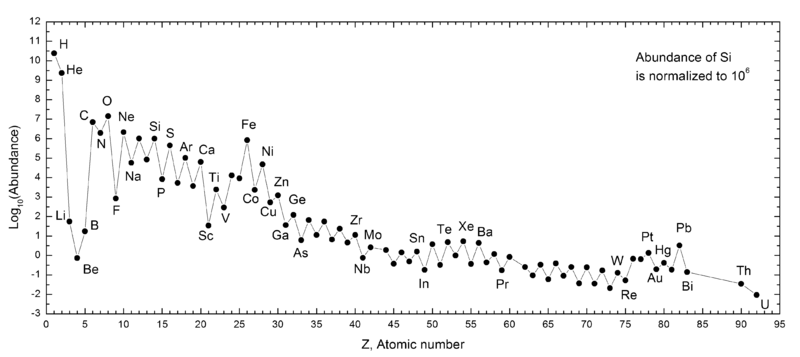
Note the log scale on the y-axis, so each change in the number by 1 is in fact
a factor of 10!