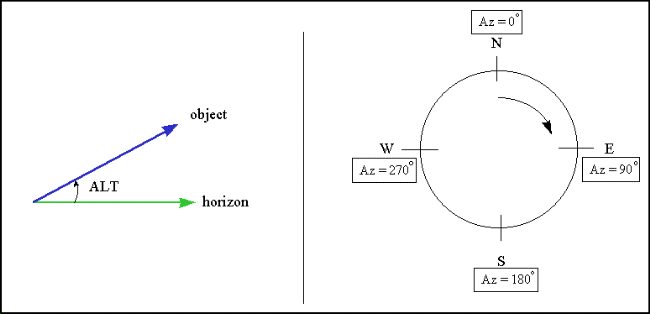
In the previous two classes we have been developing the
techniques and language that will allow us to understand how and why
celestial objects move the way they do. We talked about azimuth and elevation.
These are the only two angles you need to know to point to a specific object in
the sky. Elevation also goes by the name "altitude". Here is a diagram showing
how these two angles are defined:

These two quantities are referenced to your local horizon. The position of a celestial object in the sky depends on the time of day, and changes depending where you are on the Earth. Let's examine this finding a little closer. If we go back to about 600 BC, back to the rise of Thales and his school, it was believed that the Earth was flat--usually a disk, surrounded by water. But as humans began to roam more freely over the globe, someone noticed that they could see different stars as they went to the north or the south. If they traveled north, the north star (Polaris) would be higher in the sky (its altitude was larger). If they traveled to the south, new stars--at least ones they were not familiar with--would appear on the southern horizon. How could this be explained? For if the world was flat, then all stars would be visible at all places at any particular time.
An awakening takes place somewhere around 550 BC that a disk/flat Earth model does not work. For example, if you look at the Sun and the Moon, they are both circular all of the time. Unless our viewing angle never changed, and the Sun and the Moon decided to keep the same exact orientation all of the time, this was not possible. A better explanation was that the Sun and Moon were spheres. They also could now explain the phases of the Moon as due to a changing angle with respect to the Sun, as the shapes exhibited by the Moon were ones that could be reproduced using a sphere and a light source. We will talk about this in the next class. So, it was soon proposed that the Earth, Sun and Moon were all spherical in nature. In fact an entire Greek cult, lead by Pythagoras, grew up around this premise, and found a school of thought based on perfect shapes and numbers (Pythagoras is, of course, famous for his theorem about the sides of a triangle). The ideas of this cult, even though heavily ridiculed by their contemporaries and by those that followed (such as Plato and Aristotle), actually heavily influenced later thought. The idea that the sphere was perfection took hold, and an entire cosmology--a model for the Universe as a whole--grew out of these ideas.
In this model, the stars themselves were attached to a crystalline sphere that circled the Earth once every day. But not exactly once every day, since the stars changed on a seasonal time scale. The Sun and Moon were also attached to crystal spheres. The Sun revolved around the Earth once per day, but also slowly moved with respect to the background stars. The Moon was located close to Earth and moved more quickly. The five planets (Mercury, Venus, Mars, Jupiter and Saturn) were located further from Earth than the Moon--Mercury and Venus were believed to be on their own spheres between the Moon and the Sun, while the other planets were on more distant spheres.
This model, the "Geocentric model" of the Universe, was the one that quickly took hold in the ancient world. As with about all scientific, moral, and political matters, the views believed and expressed by Aristotle would be the ones accepted by the ancient world, most of which would not be discarded for 2000 years! The Aristotelian, geocentric view of the Universe can be summarized by the following:
"Aristotle ... put forward his notion of an ordered universe or cosmos. It was governed by the concept of place, as opposed to space, and was divided into two distinct parts, the earthly or sublunary region, and the heavens. The former [earthly] was the abode of change and corruption, where things came into being, grew, matured, decayed, and died; the latter was the region of perfection, where there was no change. In the sublunary region, substances were made up of the four elements, earth, water, air, and fire. Earth was the heaviest, and its natural place was the center of the cosmos; for that reason the Earth was situated in the center of the cosmos. The natural places of water, air, and fire, were concentric spherical shells around the sphere of earth. Things were not arranged perfectly, and therefore areas of land protruded above the water. Objects sought the natural place of the element that predominated in them. Thus stones, in which earth predominated, move down to the center of the cosmos, and fire moves straight up. Natural motions were, then, radial, either down or up. The four elements differed from each other only in their qualities. Thus, earth was cold and dry while air was warm and moist. Changing one or both of its qualities, transmuted one element into another. Such transmutations were going on constantly, adding to the constant change in this sublunary region.The heavens, on the other hand, were made up of an entirely different substance, the ether or quintessence (fifth element), an immutable substance. Heavenly bodies were part of spherical shells of ether. These spherical shells fit tightly around each other, without any spaces between them, in the following order: Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, fixed stars. Each spherical shell (hereafter, simply, sphere) had its particular rotation, that accounted for the motion of the heavenly body contained in it. Outside the sphere of the fixed stars, there was the prime mover (himself unmoved), who imparted motion from the outside inward. All motions in the cosmos came ultimately from this prime mover. The natural motions of heavenly bodies and their spheres was perfectly circular, that is, circular and neither speeding up nor slowing down."1

But it was apparent to a trained observer that this model could not be completely true. For if one carefully watched the motions of the planets over the year, they would soon find that the planets did not move at a constant rate across the sky--in fact, sometimes the planets appeared to go backwards! Here is an example of the motion of Mars:
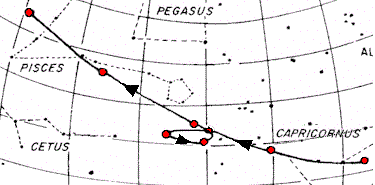
Mars, and all of the other planets appear to move among the background stars at different speeds depending on where they are in the sky (the Sun and Moon also have changing speeds across the sky, but these are too small for the casual observer to notice). Generally, all of the planets (except Mercury and Venus) slowly move eastward. Then all of a sudden they start to slow down, then go backwards for a short time, and then turn around and continue their "normal" motion. How could this be possible in the view of Aristotle? Well, it wasn't---most of the philosophers of the time simply ignored it, figuring it was just due to the strange perceptions of nature peculiar to humans--the Universe was perfectly ordered, so such motions could not be real! But astrologers could not ignore this, as the positions of the planets was vital to predict the future. Something had to be done. They needed to be able to predict the motion of the planets both forward, and backwards in time.
It was left to Claudius Ptolemy (85 to 165 AD) to rescue the geocentric model by coming up with a number of tricks to help explain the planetary motion, and enable the prediction of the positions of the planets at anytime in the future and into the past. How did he do this? His first trick was to put the Earth slightly off-center from the center of a particular planet's sphere, called the "eccentric":
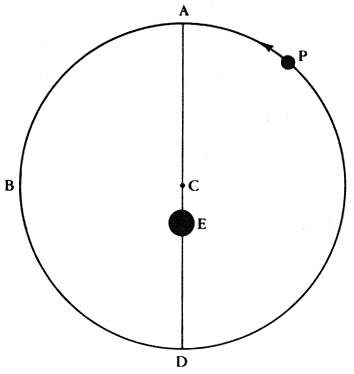
This change allowed for changing speeds as the planet's distance would not be constant, thus it would appear to go faster, and/or slower depending on where it was in its "orbit". But this could not make a planet move backwards, so Ptolemy had to come up with another device, the "epicycle":
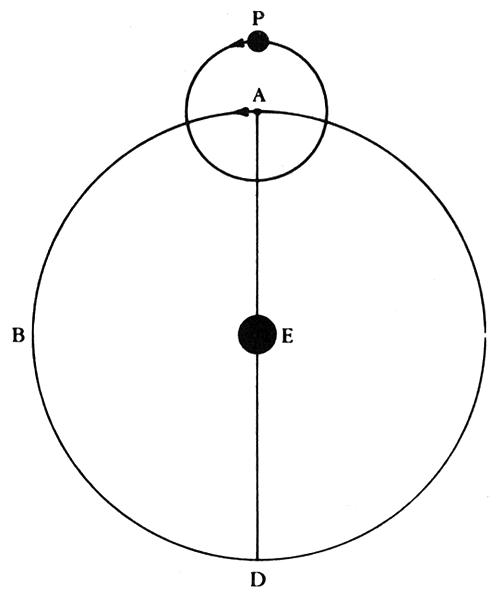
The planet would actually be attached to a smaller sphere that itself was attached to a larger sphere. The larger sphere would slowly rotate, and the smaller sphere would also rotate. Thus, the epicycle itself would move in a relatively uniform way around the center of the crystalline sphere, and this motion would result in the planet appearing to move backwards at times. The combination of the eccentric and epicycle nearly fixed the motions of all of the planets, but he needed one more little device, called the "equant":
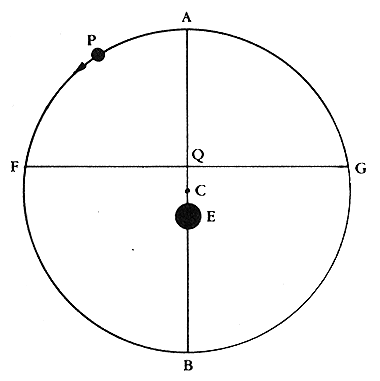
The equant point was a complicated notion that the center point of the epicycle would move uniformly around the equant point "Q" (and not the center of the larger sphere that was offset from the Earth!). This is a complicated system, but it could finally explain the motions of the planets better than any that had come before it. The sum of all of these motions is shown here:
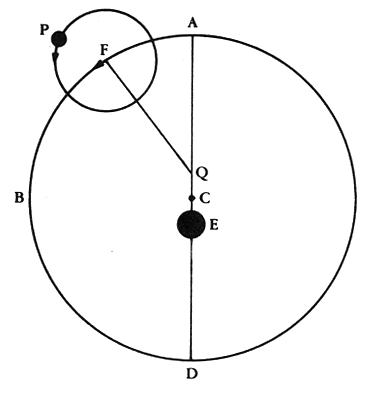
These tricks greatly offended the philosophers of the day--they suggested that the Universe was not perfect, and thus while the Ptolemaic system actually predicted the postions of the planets with great accuracy, it was relegated to a much lower position of respect than the Aristotelian view. The latter was considered to be the "true" model of the Universe, while Ptolemy's model was relegated to purely mechanics. It couldn't be correct since the Universe was perfect--it was merely a way for humans to figure out how to predict where the planets appeared to be in the sky. Ptolemy's tricks worked so well, however, that his model was not seriously challenged for 1,500 years!
The travels and explorations of humans certainly lead to some revolutionary astronomical ideas, such as the notion that the Earth was a sphere, as were the Sun and Moon. Physical objects, made of various different substances, that were in actual motion around the Earth. While we may laugh at these ideas now, you must realize how important such a shift in perception actually was. You could now understand the motions of these celestial objects--you had a model. They were no longer some mystical gods with unknowable properties. They were "real" objects.
Exploration of our planet was starting to take place, and with that began trade with farflung locations. To carry on this trade, you had to know how to navigate from one point to another. This required a deeper understanding of the Earth and the sky. One of the most important measurements of ancient times is that of the size of the Earth by Erastothenes (276 to 194 BC). Erastothenes was born in Cyrene, in modern day Libya:
"Eratosthenes made a surprisingly accurate measurement of the circumference of the Earth. Details were given in his treatise "On the measurement of the Earth" which is now lost. However, some details of these calculations appear in works by other authors such as Cleomedes, Theon of Smyrna and Strabo. Eratosthenes compared the noon shadow at midsummer between Syene (now Aswan on the Nile in Egypt) and Alexandria. He assumed that the sun was so far away that its rays were essentially parallel, and then with a knowledge of the distance between Syene and Alexandria, he gave the length of the circumference of the Earth as 250,000 stadia.
Of course how accurate this value is depends on the length of the stadium and scholars have argued over this for a long time. It is certainly true that Eratosthenes obtained a good result, even a remarkable result if one takes 157.2 metres for the stadium as some have deduced from values given by Pliny. It is less good if 166.7 metres was the value used by Eratosthenes.
[If 157.2 m, then C = 39,300 km; if 166.7 m, C = 41,675 km. Modern value C = 39,940 km.]
Several of the papers ... discuss the accuracy of Eratosthenes' result. ... Rawlins argues convincingly that the only measurement which Eratosthenes made himself in his calculations was the zenith distance on the summer solstice at Alexandria, and that he obtained the value of 7o 12'. Rawlins argues that this is in error by 16' while other data which Eratosthenes used, from unknown sources, was considerably more accurate."2
Thus, for the first time in recorded history, the true size of the Earth is
now known. [Interestingly,
Erastothenes makes another contribution to science:
he correctly sketched the route of the river Nile and suggested that lakes
were the source of the Nile, and also correctly proposed that heavy rains
sometimes fell near the source of the Nile and it was these rains that
caused the seasonal flooding.] It would be many centuries before the entire
globe was explored, but trading between cities and countries was rapidly
expanding, and this required better navigation techniques, and closer
observations of the stars.
Let us now go back and examine the behavior of Polaris. If you take a long-exposure photograph of the night sky with your camera pointed towards Polaris,
you will get a picture that looks like the following (or as seen on page 34 of
the text):

Polaris is the dot near the center of this image (the dotted lines are the paths of airplanes that happened to cross the field during the long exposure). Note that all the other stars seem to trace arcs around Polaris, while Polaris itself stays almost fixed at the same position. Polaris does not move very much at all, and thus can be used to define a direction--North. The reason for this, of course, is that the Earth is spinning, and Polaris is located near the axis of this rotation---though this is not what the ancients believed (the Earth did not move in the geocentric model). Because Polaris appears to be motionless, it can be used as a navigational aid. If the sky is clear, you can always find the direction of North at night. Thus, sailors could use Polaris to sail their boats in the correct direction.
But Polaris is even more useful than that: it could actually tell you where you were on Earth--at least in the north-south direction. No matter where you live in the northern hemisphere, Polaris stays fixed at the same altitude for your location every single day of the year. As you travel to the North, Polaris gets higher and higher in the sky. If you travel to the South, Polaris gets lower and lower in the sky. The altitude of Polaris allows you to figure out how far North or South you are. In modern language it allows you to determine your latitude. Latitudes are measured from the equator, where the latitude is defined to be 0o, and increases to 90o at the North pole (-90o at the South pole). Of course, to define where you are in the East-West direction you need another coordinate, the one we call longitude (text fig. 2.10):
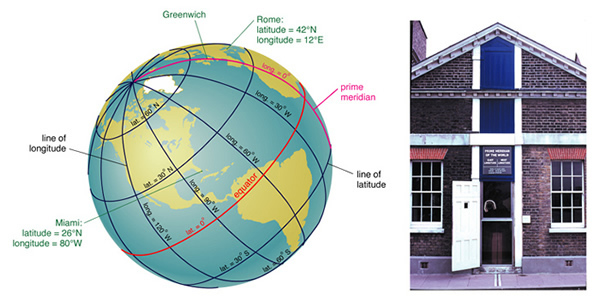
Longitude is much harder to determine than latitude. The problem with longitude is that you need to have an accurate clock. For example, if you lived on the equator and the Sun rose at 6 AM on some particular date, the Sun would rise one hour later at a point 1,666 km further to the west if it was also on the equator (40,000km/24 hours = 1,666 km/hr). But this is not very useful for determining where your ship is if you do not know what time it is! You could always figure out what time it was by determining when the Sun rose or set, or when it reached noon--but this is the local time. You do not know where you are without knowing what time it is at "home". So, until the 18th century, most long-distance sailing was done by following the coast using landmarks.
Like latitude, there has to be a zero of longitude, and this spot is defined by the Greenwich Observatory near London. Longitude is then defined as how many degrees you are east or west of the "prime meridian". Note that while a degree of latitude is the same no matter where you live on the planet (that is there are about 109 km per degree of latitude), the degrees of longitude correspond to smaller, and smaller distances as you move towards the north (or south) pole. Near the equator, one degree of longitude is about 110 km, at the latitude of Las Cruces (32.5o), one degree of longitude is about 93 km. By the time you get to the pole, the lines of longitude converge, and the separation is zero.
So, how do you measure your longitude? Well if you have a clock set to Greenwich Mean Time (GMT--the time at the prime meridian), noon on that clock means that the Sun will be due south at Greenwich. If on that clock you find that the time of local noon is 7 pm, then you are 7 hours from Greenwich. If there are 24 hours in a day, and this corresponds to 360o, then there are 15 degrees of longitude per hour of time difference. Thus, your longitude would be 7 X 15 = 105o West of Greenwich. If your local time at noon was 10AM GMT, you would be 2 X 15 = 30o east of Greenwich, so your longitude would be 30o East.
1 From the Ptolemaic System http://es.rice.edu/ES/humsoc/Galileo//Things/ptolemaic_system.h tml
2From http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Eratosthenes.html