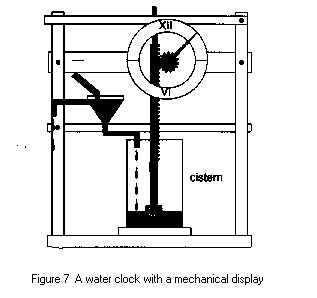
In this clock, water slowly fills the cistern, and the float rises
causing the gear to move, and make the hand circle the dial.
In the last class, we imagined we were prehistoric humans living in caves, and wondering about the mysteries of celestial events and cycles. We then rapidly progressed through human history, discussing the rise of agriculture, and how it almost certainly lead to the development of astrology and astronomy. Today we will pretend we are still living in the distant past, but now at a time when we have writing and simple arithmetic and geometry. The first writing is the Sumerian cuneiform that dates back to about 5,000 BC. Sumer was an ancient kingdom located in modern-day Iraq that was superceded by the Assyrians and Babylonians. By 3,000 BC arithmetic and geometry were widespread in the Middle East. For example, the Egyptians were using simple geometric principles to construct large monuments, such as the pyramids at Giza.
So today, we will assume that we know how to write and do simple mathematics. This will allow us to keep records of the sky, as well as draw maps, give objects names, and measure angles and time intervals. Let's start by using the sky charts in the back of your lab manual. The sky charts in your lab manual have been constructed so that they represent the sky above Las Cruces at 9pm on the 15th of each month. In these maps, North is at the top, South at the bottom, East is to the left, and West is to the right. A line drawn from the top of the chart to the bottom of the chart that bisects the sky map exactly is called the "meridian". The meridian is a line that goes from North to South, passing straight overhead---it is equivalent to the Longitude of your position on Earth, and it does not move. So, we could put two sticks in the ground that are lined-up exactly on this north-south line. These sticks would then allow us to determine when an object---such as the Sun, Moon, planet, or a particular star is due South of you--that is the "star is on the meridian".
Ok, with the definition of meridian, let us now start watching celestial objects. Let us first start with the stars using the Astronomy 110 star charts. Let us look at the sky chart for December. Notice that the constellation Orion (which we discussed last class) is to the left of the meridian: "On December 15th, at 9 pm, the constellation Orion is east of the meridian".
Let us now look at the chart for January. On January 15th, Orion is almost on the meridian, but it is still slightly east of the meridian at 9pm. Looking at February we now find that Orion is to the west of the meridian at 9pm on the 15th! Note that the distance of Orion from the meridian is about the same in January and February. In fact, Orion is exactly on the meridian at 9pm on January 30th. Let's look at one more chart, that for March . In March, Orion is well to the west of the meridian at 9pm.
What have we discovered? The constellations move with the passage of time! Note that the individual stars do not move--the constellations we see today look nearly identical to those seen by the ancient Greeks--it is the entire constellations that move (the actual stars themselves do in fact move, but at a rate that is imperceptible over human lifetimes). In the winter time, Orion is visible in the evening sky, but by Spring, it is no longer visible to us. Thus, there are "winter constellations", "summer constellations", "spring constellations", and "fall constellations". For example, the Big Dipper (Ursa Major) is a spring constellation.
How can we attempt to understand what is going on here? Why are the constellations and other celestial objects constantly marching across the sky? Before we can proceed much further, we need to talk about measuring time. Note that ancient peoples did not have highly accurate ways to tell time. The more modern electric, spring or weight driven clocks (that you and I are familiar with) would not be developed for about 3,000 more years. As civilization advanced, however, it soon became necessary to tell time. For if you were a baker and were wishing to buy some grain from a farmer who had it, you needed to specify the time at which you were going to meet him to allow you to make this purchase. So, some form of time keeping had to be developed to allow business, religion and government to function smoothly.
Before we can have "time" and clocks, we must settle on some fundamental unit. This unit is obvious: the day. We define the day as the time interval that elapses between successive sunrises. Nearly, all animal and plant life is keyed to this unit. Some animals only come out at night, while most human activities occur during the daylight hours. This was especially true in the past, when only crude forms of lighting (candles/oil lamps) were available. It is obvious, however, that we need a smaller unit of time than a day. If I said "I will meet you tomorrow at the Acropolis", it could mean that I will show up at dawn, or right before sunset! Very inconvenient.
It is quickly apparent that there has to be some midpoint between the time of sunrise and sunset. We call this time "noon". The Sun rises in the East, crosses the sky reaching its highest point above the horizion at noon, and sets in the West. At noon, the Sun is due South. Using our language defined earlier, we say that the Sun is on the meridian at noon. Now we have come up with a way to divide the daytime into two parts--before noon ("Ante Meridian" = AM), and after noon ("Post Meridian": PM).
How can we tell when noon occurs? If we draw the north-south line in the dirt, and then erect a (perfectly vertical) stick, then at noon, the shadow of this stick will line-up with the north-south line (i.e., the meridian!). Now we have a way to determine the time of noon. The vertical stick is called a "gnomon". Now let's look at how the shadow of the gnomon progresses throughout the day. When the Sun rises in the morning, it rises in the East, so the shadow of the gnomon would fall to the West. As morning progressed, the shadow would slowly move from the west, towards the north, falling right on the meridian at noon. After noon, the Sun would now be west of the meridian, so the shadow would progress from the meridian to the east. When the Sun set in the west, the shadow of the gnomon would fall to the east. This would happen every day. Here is an animation.
It is pretty obvious, that all we had to do was divide this path up into smaller units, and we could now tell time during the day! The first Sun clocks based on vertical gnomons were constructed about 3500 BC. The (more) modern sundial (with a tilted gnomon) grew out of these first efforts. By 1500 BC, the Egyptians had divided the day into 10 parts, plus two "twilight hours" (the times between when the first hint of sunrise is present on the eastern horizon and sunrise--"dawn", and that period after sunset until it is no longer light enough to read--"dusk").
The problem with sun clocks (besides not being useful when cloudy or at night) was the fact that the sub-units of the day---the hours---were not uniform throughout the year. As we discussed last class, at this time of year, there are about 10 modern hours of daylight. In June, there are 14 hours of daylight, in January there are 10 hours of daylight. Thus, the "sun hours" in June are 1.4 times as long as they are in January! Still, such clocks were good enough to conduct business, as all of the sun clocks in the city would still read the same time on any particular date. So if you now said you would meet your friend at the Acropolis at one hour past noon tomorrow, you would both arrive at the correct time since there were such clocks located throughout the cities of the ancient world.
By watching the stars, ancient astronomers were also able to tell time at night by measuring the motions of various constellations--such as the Big Dipper. They could make tables of the times during the year when a certain star in the Big Dipper crossed the meridian. But this required careful observations, and was not a practical way to keep time for the average citizen.
Soon, better methods of keeping time were developed. The first of these were water clocks. The first water clocks appear to have been developed around 1500 BC. A water clock is a simple device in that it consists of a reservoir of water in which a small hole is drilled, and the water slowly leaks out and fills a bowl or some other container, in which there are marks drawn that correspond to the hours (this can also be done with sand, like the common egg timer). The technology of water clocks advanced quite quickly, and soon enormous buildings were constructed to house these devices, and large dials were turned that allowed everyone to read them from a long distance---we now had fairly accurate, practical, and uniform way to measure time. Here are two examples, one small and simple, and one much larger:

In this clock, water slowly fills the cistern, and the float rises
causing the gear to move, and make the hand circle the dial.

Because we can now tell time, we can get back to
trying
to understand the various types of celestial motion! Since we have
abandoned
the Sun clock, we can now investigate how the length of the day changes
throughout the year. Let's say we have a good water clock, and
carefully
record the times of sunrise and sunset throughout the year in Las
Cruces.
Here is a table of these times (we will ignore the modern convention of
Daylight savings time):
| Date | Sunrise | Sunset | Daylight Hours |
| January 1st | 7:09 AM | 5:13 PM | 10.1 |
| February 1st | 7:02 AM | 5:41 PM | 10.7 |
| March 1st | 6:35 AM | 6:05 PM | 11.5 |
| April 1st | 5:56 AM | 6:27 PM | 12.5 |
| May 1st | 5:21 AM | 6:48 PM | 13.5 |
| June 1st | 5:01 AM | 7:09 PM | 14.1 |
| July 1st | 5:04 AM | 7:18 PM | 14.2 |
| August 1st | 5:22 AM | 7:05 PM | 13.7 |
| September 1st | 5:42 AM | 6:32 PM | 12.8 |
| October 1st | 6:01 AM | 5:52 PM | 11.9 |
| November 1st | 6:24 AM | 5:17 PM | 10.9 |
| December 1st | 6:51 AM | 5:02 PM | 10.2 |
You can see that the shortest days are in December and January, while the longest days are in June and July. In late December, there are 10 hours of daylight, and in late June there are 14 hours of daylight. Why does this happen? This is the first big puzzle we need to solve. To do so, however, we need to incorporate other types of measurement-- one regarding WHERE objects appear to rise and set, as well as how high they get in the sky.
We have already been casually using the terms North, South, East, and West without really defining what they mean. To do so we must bring in a little geometry. We have defined the meridian as the line that passes from due north, passing through your position, and continuing to due south. Due south is defined as that point where the Sun reaches its highest point in the sky (at least for those in North America, Europe and Asia). We have said that the Sun rises in the East, and sets in the West. But this is not a very precise definition, because if you actually chart the position where the Sun rises throughout the year, you will see if shifts back and forth along your eastern horizon (as the position of sunset does on the western horizon).
The Cardinal Directions and the Definition of Azimuth
A better way to define the directions of East and West is to draw a line that is perpendicular to the meridian. That is, the East-West line will be at right angles to the North-South line. You are familiar with this set-up, as this is used in compasses:

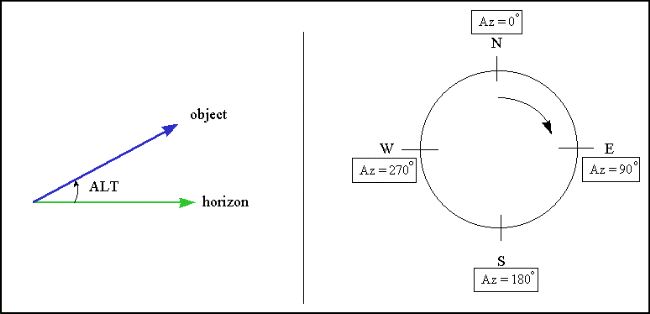
These angular measurements around the horizon are called "azimuths". We say that the azimuth of South is 180o. Now, we can talk about an object at an azimuth of 45o, which corresponds to Northeast (NE), or at any azimuth in between. Now, let's look at the azimuths of sunrise and sunset at four times during the year in Las Cruces:
March 21st: Sunrise azimuth = 90, sunset azimuth =
270.0
June 21st: Sunrise azimuth = 61.78,
sunset azimuth = 298.22
September 21st: Sunrise azimuth = 90, sunset azimuth
= 270.0
December 21st: Sunrise azimuth = 118.22, sunset azimuth
= 241.78
Why did I pick these dates? Well, of course--they are the dates that mark the start of the four seasons. Note that there are two special dates (and only two!) during the year when the Sun rises at an azimuth of 90o, and that is in March and September. Remember that 90o corresponds to due East! Between the dates of March 21st and September 21st, the azimuth of sunrise is smaller than 90o, that is, it is to the North of East (northeast), and between the dates of September 21st and March 21st the azimuth of sunrise is to the South of East (i.e., southeast). You can also note that the sunsets mirror the sunrises, in that during spring and summer, the sun sets to the north of west (northwest), and during the fall and winter, the sun sets to the south of west (southwest).
Ancient peoples also recognized this apparent motion of the sun along their horizon. For example, at Stonehenge in England (see page 94), and at Chaco Canyon in New Mexico, large stone structures were constructed and oriented to mark the location of sun rises at the extremes in their motions (as well as the one at due East). June 21st signaled the furthest northeastern position of sunrise, while six months later, on December 21st, the sunrise occured at its most southeastern location. Why did these ancient peoples worry about this? Of course, it is related to agriculture. They needed to keep track of the seasons so they knew when to plant their crops. The Anasazi in New Mexico did not have a Nile that flooded! So they needed a different system, one where their only clues about the seasons came from watching the skies. They needed a way to keep track of the celestial motions without having to do a lot of record keeping.
If you built a structure that would allow you to determine when Spring occurred, the time when you want to plant your crops, all you had to do was occasionally visit this structure, and you would quickly know what time of the year it was by determining where the sun rose on your horizon. These were like calendars on a huge scale, and eliminated having to keep written records to track of the passage of time. You had more important things to do than that! These types of structures started appearing all over the globe by 5,000 BC.
Before we leave the subject of the motion of the sun along the horizon, we should introduce two more terms which you have surely heard used: equinox and solstice. The term equinox, usually used together with spring and autumn ("spring equinox", "autumnal equinox"), literally means that night and day have the same length. If you notice back on our table of sunrises and sunsets, at the start of spring and fall (March 21st and September 21st, respectively), daylight lasts exactly 12 hours, and night time lasts exactly twelve hours. Thus night and day are the same length. Solstice literally means "the sun stands still". We have both summer and winter solstices. If you watch the progression of the sunrise along the horizon, after the start of spring, they continually move north until the start of summer, after which the sunrises star moving south again. The northern-most point of this motion is where the sun stops, and then turns around and heads back the other way in its apparent motion along our horizon. Thus the term solstice. In the winter the opposite happens. The southern-most point in the sun's motion along the horizon is the time of the "winter solstice".
Now, as society progressed, and kings hired priests and astronomers to keep track of time, record keeping was no longer so onerous, and other important celestial motions could be observed. It was quickly realized that the sun's motion along the horizon at sunset and sunrise repeated year after year. In fact, the ancients noticed that the time it took for the sun to complete its travels from the point of winter solstice to summer solstice, and back to winter solstice again, required 365 days. This cycle is, of course, the length of our year.
The Origin of Months
The various ancient cultures devised further subdivisions of the year, which we call months. As the name suggests, the word month is derived from the word "Moon". So far, all we have talked about is the motion of the Sun in the sky, and not worried about much else. But the Moon is bright, of course, and its motion through the sky was also followed carefully. They noticed that it would first appear in the evening sky as a thin crescent. As the days progressed this crescent would grow until the disk of the moon was a complete circle ("full moon") and rose in the east at sunset, and then the cycle would reverse, and the moon would shrink to a thin crescent that would be visible just before sunrise, where it would disappear from sight for two or three days, and then suddenly appear in the western sky again. The time of disappearance was called "new moon", as the moon would appear to be reborn so that it could begin a new cycle. The ancient astronomers quickly noticed that 29.5 days elapsed between two successive full moons, or two new moons. As the length of this cycle is close to 30 days, and the fact that 30 is easily divided into 360 days (360 divided by 30 = 12), a new unit of time was devised called the month, based on the lunar cycle.
Unfortunately, the lunar motion was not devised by a human, so our system needs some adjustments. For example, if we multiply 29.5 days X 12 months we end up with 354 days. This is 11 days shorter than the year. Some ancient cultures had 12 normal months, and then a short month before the start of the next cycle/year. But there were some cultures that based their calendar on longer cycles--for example, the Hebrew calendar. It was noticed that the full moon would occur on the same calendar date after 19 years. Let's look at this more closely. The year has 365 days, thus 19 years would be 19 X 365 = 6,935 days. If you divide this number by 29.5, you get the result of 235.085. Thus, there are almost exactly 235 lunar "months" in 19 years. Because of this, the date of full moon repeats on a 19 year cycle. For example, there was a full moon on the 25th of January in 2005. There will again be a full moon on January 25th, 2024.
Modern Months and Leap Years
In modern times, we have adjusted the lengths of our months to better correspond to our year. Instead of having twelve months of 30 days, we have seven months of 31 days (217 days), four months of 30 days (120 days), and one month of 28 days: 217 + 120 + 28 = 365. But you may ask, what is this leap year thing that seems to happen every once and a while? During a leap year, February has 29 days, and thus the year is 366 days long. Why does this happen? It was already known by 3,000 BC that the year was not in fact 365 days long, but actually 365.25 days long--yes, they were good enough observers to measure this! Of course, it doesn't take great observational expertise to determine this, just fairly good record keeping. For example, if we construct our observatory so that the exact location of East is known to us, we can keep track of how long it takes between successive sunrises at this spot.
Because the year is not exactly some perfect multiple of a day, this extra time will eventually add up to something much larger. For example, given that the year is 365.25 days long, let's look at what will happen on long term cycles. We measure the date when the sunrise occurs at an azimuth of 90 degrees--let's call this March 21st, 2003. After 365 days have elapsed we go out to measure where the sun rises on March 21st, 2004. We notice that it has risen at a spot slightly to the south of east, if we could accurately measure it, the azimuth would be at number like 90.04 degrees. In 2005 we find that on the 21st of March the sun rises even further to the south. On the 21st of March 2006 it is even further to the south, and so on. It gets so bad that by 2007, the sun does not rise at an azimuth of 90 degrees until the 22nd of March--it is one day late on its journey north! In the year 2011, the sun would not rise at an azimuth of 90 degrees until March 23rd. You see what is happening? The sun is one day late after four years, two days late after eight years, three days late after 12 years, etc. In 100 years, the sun would be 25 days late, and spring would now occur in April!
So, it did not take the ancient astronomers too long to figure out that the length of the year was not a perfect mulitple of the length of our day. They quickly determined that the year was closer to 365.25 days long. The modern value for the length of the year is 365.2422 days. Note that the leap year system works pretty well, but after very long times, that tiny bit of remainder (0.0078) starts to affect things. For example, after 1000 years, it amounts to 7.8 days. Our calendar has a mechanism to account for this effect too: a leap year occurs every four years, except at the change of a century, unless that century is evenly divisible by 400. If this latter adjustment didn't occur, then each 1,000 years would see 250 leap days added, when you only wanted to add 242 leap days. So we need to remove eight leap days, and that is why only centuries divisible by 400 are leap years (this occured in 2000, and will occur in 2400, and again in 2800--see now we only have 3 leap days per 1,000 years added at the turn of centuries instead of 10. If you are interested in reading more about this topic, our textbook has a special chapter that describes these things.
Elevation Angle
Before we finish this, lets talk about another type of angular measurement. So far, we've been talking about azimuth--the angle that something has at our horizon. But there is another equally important angle: elevation angle, the distance that an object is above our horizon. For example, at the horizon, an object has an elevation angle of 0o while something straight overhead has an elevation angle of 90o. Let's apply this to the apparent motion of the sun. In Las Cruces, the sun has an elevation angle of 34o at noon on December 21st. On June 21st, the sun has an elevation angle of 81o at noon. The sun is much higher in the sky (almost straight overhead) in June then it is in December. The largest possible elevation angle is 90o. For example, we say that the sun is 81o above the southern horizon at noon on June 21st. We do not say that the sun is 99o above the northern horizon.
How are elevation angles measured? The best way is to use a device called a sextant:
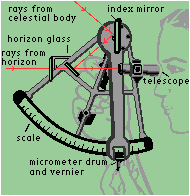
Sextants were used by navigators to figure out their location. How is this possible? On page 34 in your text there is a long-exposure photograph of the northern sky. The stars in this photograph trace out arcs over the four hours of the photograph (the stars move across the sky just like the sun does). Each 24 hours, the stars complete one circuit around the sky. Here is another such photograph:

Note that one star near the center of the photograph does not move very much at all, in fact the other arcs are "concentric" around this point. This star is the north star--Polaris. If you were sitting on the north pole of the Earth, Polaris would be straight overhead, that is it would have an elevation angle of 90o. At the Earth's equator, however, Polaris would have an elevation angle of 0o (and probably not be visible unless you were on a high mountain). In Las Cruces, Polaris always has an elevation angle of 32.5o above the northern horizon. Does that number sound familiar? In fact, that is the "latitude" of Las Cruces. We are 32.5o north of the equator. By measuring the elevation angle of Polaris, you can figure out your latitude on Earth (besides knowing which direction North is!).
In previous classes we have been developing the
techniques and language that will allow us to understand how and why
celestial objects move the way they do. We talked about azimuth and elevation.
These are the only two angles you need to know to point to a specific object in
the sky. Elevation also goes by the name "altitude". Here is a diagram showing
how these two angles are defined:
These two quantities are referenced to your local horizon. The position of a celestial object in the sky depends on the time of day, and changes depending where you are on the Earth. Let's examine this finding a little closer. If we go back to about 600 BC, back to the rise of Thales (died 546 BC) and his school in Miletus (now in Turkey), it was believed that the Earth was flat--usually a disk, surrounded by water. But as humans began to roam more freely over the globe, someone noticed that they could see different stars as they went to the north or the south. If they traveled north, the north star (Polaris) would be higher in the sky (its altitude was larger). If they traveled to the south, new stars--at least ones they were not familiar with--would appear on the southern horizon. How could this be explained? For if the world was flat, then all stars would be visible at all places at any particular time.
An awakening takes place somewhere around 550 BC that a disk/flat Earth model does not work. For example, if you look at the Sun and the Moon, they are both circular all of the time. Unless our viewing angle never changed, and the Sun and the Moon decided to keep the same exact orientation all of the time, this was not possible. A better explanation was that the Sun and Moon were spheres. They also could now explain the phases of the Moon as due to a changing angle with respect to the Sun, as the shapes exhibited by the Moon were ones that could be reproduced using a sphere and a light source. We will talk about this in coming classes. So, it was soon proposed that the Earth, Sun and Moon were all spherical in nature. In fact an entire Greek cult, lead by Pythagoras (569 - 475 BC) grew up around this premise, and found a school of thought based on perfect shapes and numbers (Pythagoras is, of course, famous for his theorem about the sides of a triangle). The ideas of this cult, even though heavily ridiculed by their contemporaries and by those that followed (such as Plato and Aristotle), actually heavily influenced later thought. The idea that the sphere was perfection took hold, and an entire cosmology--a model for the Universe as a whole--grew out of these ideas.
In this model, the stars themselves were attached to a crystalline sphere that circled the Earth once every day. But not exactly once every day, since the stars changed on a seasonal time scale. The Sun and Moon were also attached to crystal spheres. The Sun revolved around the Earth once per day, but also slowly moved with respect to the background stars. The Moon was located close to Earth and moved more quickly. The five planets (Mercury, Venus, Mars, Jupiter and Saturn) were located further from Earth than the Moon--Mercury and Venus were believed to be on their own spheres between the Moon and the Sun, while the other planets were on more distant spheres.
This model, the "Geocentric model" of the Universe, was the one that quickly took hold in the ancient world. As with about all scientific, moral, and political matters, the views believed and expressed by Aristotle (384-322 BC) would be the ones accepted by the ancient world, most of which would not be discarded for 2000 years! The Aristotelian, geocentric view of the Universe can be summarized by the following:
"Aristotle ... put forward his notion of an ordered universe or cosmos. It was governed by the concept of place, as opposed to space, and was divided into two distinct parts, the earthly or sublunary region, and the heavens. The former [earthly] was the abode of change and corruption, where things came into being, grew, matured, decayed, and died; the latter was the region of perfection, where there was no change. In the sublunary region, substances were made up of the four elements, earth, water, air, and fire. Earth was the heaviest, and its natural place was the center of the cosmos; for that reason the Earth was situated in the center of the cosmos. The natural places of water, air, and fire, were concentric spherical shells around the sphere of earth. Things were not arranged perfectly, and therefore areas of land protruded above the water. Objects sought the natural place of the element that predominated in them. Thus stones, in which earth predominated, move down to the center of the cosmos, and fire moves straight up. Natural motions were, then, radial, either down or up. The four elements differed from each other only in their qualities. Thus, earth was cold and dry while air was warm and moist. Changing one or both of its qualities, transmuted one element into another. Such transmutations were going on constantly, adding to the constant change in this sublunary region.The heavens, on the other hand, were made up of an entirely different substance, the ether or quintessence (fifth element), an immutable substance. Heavenly bodies were part of spherical shells of ether. These spherical shells fit tightly around each other, without any spaces between them, in the following order: Moon, Mercury, Venus, Sun, Mars, Jupiter, Saturn, fixed stars. Each spherical shell (hereafter, simply, sphere) had its particular rotation, that accounted for the motion of the heavenly body contained in it. Outside the sphere of the fixed stars, there was the prime mover (himself unmoved), who imparted motion from the outside inward. All motions in the cosmos came ultimately from this prime mover. The natural motions of heavenly bodies and their spheres was perfectly circular, that is, circular and neither speeding up nor slowing down."1
But it was apparent to a trained observer that this model could not be completely true. For if one carefully watched the motions of the planets over the year, they would soon find that the planets did not move at a constant rate across the sky--in fact, sometimes the planets appeared to go backwards! Here is an example of the motion of Mars:
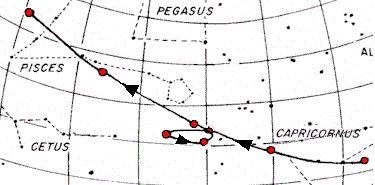
Mars, and all of the other planets (though not the Sun or Moon) appear to move among the background stars at different speeds depending on where they are in the sky. Generally, all of the planets (except Mercury and Venus) slowly move eastward. Then all of a sudden they start to slow down, then go backwards for a short time, and then turn around and continue their "normal" motion. How could this be possible in the view of Aristotle? Well, it wasn't---most of the philosophers of the time simply ignored it, figuring it was just due to the strange perceptions of nature peculiar to humans--the Universe was perfectly ordered, so such motions could not be real! But astrologers could not ignore this, as the positions of the planets was vital to predict the future. Something had to be done. They needed to be able to predict the motion of the planets both forward, and backwards in time.
It was left to Claudius Ptolemy (85 to 165 AD) to rescue the geocentric model by coming up with a number of tricks to help explain the planetary motion, and enable the prediction of the positions of the planets at anytime in the future and into the past. How did he do this? His first trick was to put the Earth slightly off-center from the center of a particular planet's sphere, called the "eccentric":
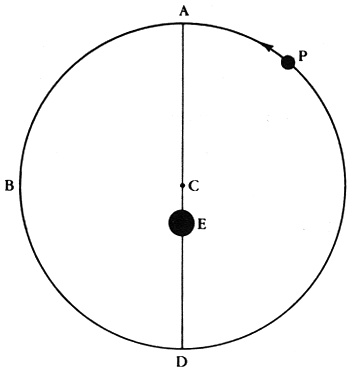
This change allowed for changing speeds as the planet's distance would not be constant, thus it would appear to go faster, and/or slower depending on where it was in its "orbit". But this could not make a planet move backwards, so Ptolemy had to come up with another device, the "epicycle":
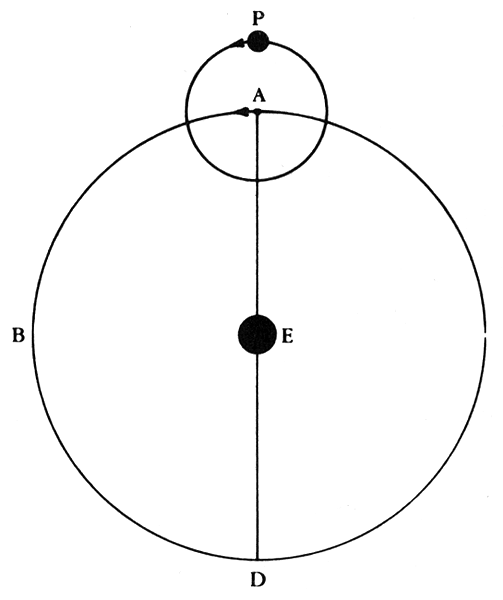
The planet would actually be attached to a smaller sphere that itself was attached to a larger sphere. The larger sphere would slowly rotate, and the smaller sphere would also rotate. Thus, the epicycle itself would move in a relatively uniform way around the center of the crystalline sphere, and this motion would result in the planet appearing to move backwards at times. The combination of the eccentric and epicycle nearly fixed the motions of all of the planets, but he needed one more little device, called the "equant":
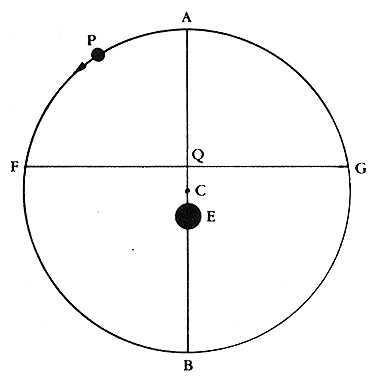
The equant point was a complicated notion that the center point of the epicycle would move uniformly around the equant point "Q" (and not the center of the larger sphere that was offset from the Earth!). This is a complicated system, but it could finally explain the motions of the planets better than any that had come before it. The sum of all of these motions is shown here:
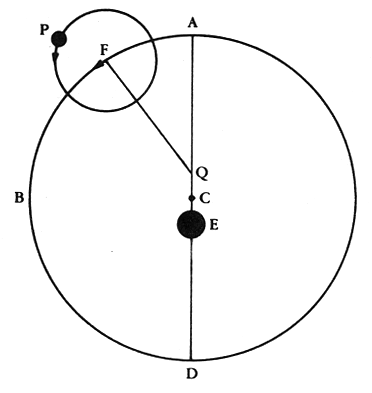
These tricks greatly offended the philosophers of the day--they suggested that the Universe was not perfect, and thus while the Ptolemaic system actually predicted the postions of the planets with great accuracy, it was relegated to a much lower position of respect than the Aristotelian view. The latter was considered to be the "true" model of the Universe, while Ptolemy's model was relegated to purely mechanics. It couldn't be correct since the Universe was perfect--it was merely a way for humans to figure out how to predict where the planets appeared to be in the sky. Ptolemy's tricks worked so well, however, that his model was not seriously challenged for 1,500 years!
The travels and explorations of humans certainly lead to some revolutionary astronomical ideas, such as the notion that the Earth was a sphere, as were the Sun and Moon. Physical objects, made of various different substances, that were in actual motion around the Earth. While we may laugh at these ideas now, you must realize how important such a shift in perception actually was. You could now understand the motions of these celestial objects--you had a model. They were no longer some mystical gods with unknowable properties. They were "real things".
Exploration of our planet was starting to take place, and with that began trade with farflung locations. To carry on this trade, you had to know how to navigate from one point to another. This required a deeper understanding of the Earth and the sky. One of the most important measurements of ancient times is that of the size of the Earth by Erastothenes (276 to 194 BC). Erastothenes was born in Cyrene, in modern day Libya:
"Eratosthenes made a surprisingly accurate measurement of the circumference of the Earth. Details were given in his treatise "On the measurement of the Earth" which is now lost. However, some details of these calculations appear in works by other authors such as Cleomedes, Theon of Smyrna and Strabo. Eratosthenes compared the noon shadow at midsummer between Syene (now Aswan on the Nile in Egypt) and Alexandria. He assumed that the sun was so far away that its rays were essentially parallel, and then with a knowledge of the distance between Syene and Alexandria, he gave the length of the circumference of the Earth as 250,000 stadia.
Of course how accurate this value is depends on the length of the stadium and scholars have argued over this for a long time. It is certainly true that Eratosthenes obtained a good result, even a remarkable result if one takes 157.2 metres for the stadium as some have deduced from values given by Pliny. It is less good if 166.7 metres was the value used by Eratosthenes.
[If 157.2 m, then C = 39,300 km; if 166.7 m, C = 41,675 km. Modern value C = 39,940 km.]
Several of the papers ... discuss the accuracy of Eratosthenes' result. ... Rawlins argues convincingly that the only measurement which Eratosthenes made himself in his calculations was the zenith distance on the summer solstice at Alexandria, and that he obtained the value of 7o 12'. Rawlins argues that this is in error by 16' while other data which Eratosthenes used, from unknown sources, was considerably more accurate."2
Thus, for the first time in recorded history, the true size of the Earth is
now known. [Interestingly,
Erastothenes makes another contribution to science:
he correctly sketched the route of the river Nile and suggested that lakes
were the source of the Nile, and also correctly proposed that heavy rains
sometimes fell near the source of the Nile and it was these rains that
caused the seasonal flooding.] It would be many centuries before the entire
globe was explored, but trading between cities and countries was rapidly
expanding, and this required better navigation techniques, and closer
observations of the stars.
Let us now go back and examine the behavior of Polaris. If you take a long-exposure photograph of the night sky with your camera pointed towards Polaris,
you will get a picture that looks like the following (or as seen on page 34 of
the text):

Polaris is the dot near the center of this image (the dotted lines are the paths of airplanes that happened to cross the field during the long exposure). Note that all the other stars seem to trace arcs around Polaris, while Polaris itself stays almost fixed at the same position. Polaris does not move very much at all, and thus can be used to define a direction--North. The reason for this, of course, is that the Earth is spinning, and Polaris is located near the axis of this rotation---though this is not what the ancients believed (the Earth did not move in the geocentric model). Because Polaris appears to be motionless, it can be used as a navigational aid. If the sky is clear, you can always find the direction of North at night. Thus, sailors could use Polaris to sail their boats in the correct direction.
But Polaris is even more useful than that: it could actually tell you where you were on Earth--at least in the north-south direction. No matter where you live in the northern hemisphere, Polaris stays fixed at the same altitude for your location every single day of the year. This is shown in the following photograph (this image was made by Photoshoping together many short exposures obtained on various nights throughout the year over Vienna):

As you travel to the North, Polaris gets higher and higher in the sky. If you travel to the South, Polaris gets lower and lower in the sky. The altitude of Polaris allows you to figure out how far North or South you are. In modern language it allows you to determine your latitude. Latitudes are measured from the equator, where the latitude is defined to be 0o, and increases to 90o at the North pole (-90o at the South pole). Of course, to define where you are in the East-West direction you need another coordinate, the one we call longitude (text fig. 2.10):
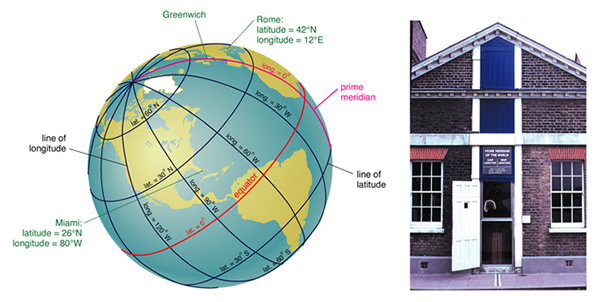
Longitude is much harder to determine than latitude. The problem with longitude is that you need to have an accurate clock. For example, if you lived on the equator and the Sun rose at 6 AM on some particular date, the Sun would rise one hour later at a point 1,666 km further to the west if it was also on the equator (40,000km/24 hours = 1,666 km/hr). But this is not very useful for determining where your ship is if you do not know what time it is! You could always figure out what time it was by determining when the Sun rose or set, or when it reached noon--but this is the local time. You do not know where you are without knowing what time it is at "home". So, until the 18th century, most long-distance sailing was done by following the coast using landmarks.
Like latitude, there has to be a zero of longitude, and this spot is defined by the Greenwich Observatory near London. Longitude is then defined as how many degrees you are east or west of the "prime meridian". Note that while a degree of latitude is the same no matter where you live on the planet (that is there are about 109 km per degree of latitude), the degrees of longitude correspond to smaller, and smaller distances as you move towards the north (or south) pole. Near the equator, one degree of longitude is about 110 km, at the latitude of Las Cruces (32.5o), one degree of longitude is about 93 km. By the time you get to the pole, the lines of longitude converge, and the separation is zero.
So, how do you measure your longitude? Well if you have a clock set to Greenwich Mean Time (GMT--the time at the prime meridian), noon on that clock means that the Sun will be due south at Greenwich. If on that clock you find that the time of local noon is 7 pm, then you are 7 hours from Greenwich. If there are 24 hours in a day, and this corresponds to 360o, then there are 15 degrees of longitude per hour of time difference. Thus, your longitude would be 7 X 15 = 105o west of Greenwich. If your local time at noon was 10AM GMT, you would be 2 X 15 = 30o east of Greenwich, so your longitude would be 30o East.
1 From the Ptolemaic System http://es.rice.edu/ES/humsoc/Galileo//Things/ptolemaic_system.h tml
2From http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Eratosthenes.html