Consider the question of stellar aberration, namely the change in the apparent position of a star due to the motion of the Earth. For a reference frame K' with coordinates (x', y', z') moving in the positive x-direction with velocity v relocate to frame K with coordinates (x,y,z), we have the Lorentz transformation relating to the coordinates as follows.

Consider a particle which has a velocity u' in the K' frame of reference. We can show that the apparent velocity in the K fame is as follows. This will result in the velocity transformations for motion parallel (u_x) or perpendicular (u_y or u_z) to the direction of motion.

We define u'_x and u'_y in terms of an angle , choosing to align our axes such that u'_z is zero. The aberration formula is then expressed in terms of tan.

For the case of the aberration of light, u' = c. In this case,

For a photon emitted at right angles to the direction of motion in frame K',

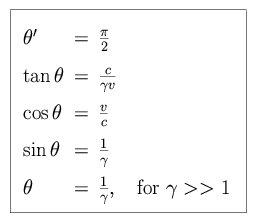This means that if photons are emitted isotropically in reference fame K', in frame K it will appear that half of the photons are concentrated in a cone of half-angle 1/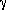 (a strong beaming effect).

Finally, consider the aberration of starlight due to the movement of the Earth around the Sun. For a frame moving with velocity v, we define the aberration angle as the difference between ' and .

We can now find the shift S in the apparent angular position of a star, as viewed from Earth at two points in time separated by three months. As the nearest star lies at a distance of 10 cm, and the Earth's orbital radius is 10 cm, the displacement of the Earth is negligible. At the first position, the Earth is moving directly toward the star. Three months later, the Earth is moving perpendicular to the vector which points toward the star.