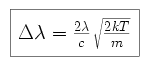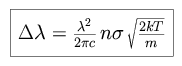Structure of Spectral Lines
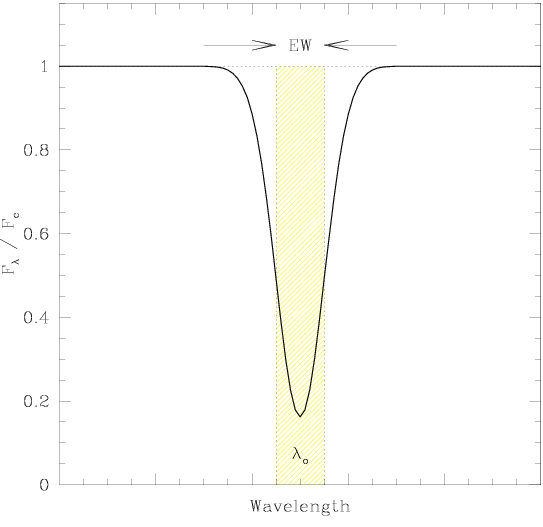
Consider the spectrum of an optically thin ( << 1) line; there is no wavelength at
which all of the radiant flux is completely blocked. The equivalent width EW
is the width (e.g., in Angstroms) the line would have if it had no wings, with
an instantaneous transition between the full continuum level to full
absorption about the central wavelength
<< 1) line; there is no wavelength at
which all of the radiant flux is completely blocked. The equivalent width EW
is the width (e.g., in Angstroms) the line would have if it had no wings, with
an instantaneous transition between the full continuum level to full
absorption about the central wavelength 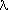 o.
o.
The opacity 
 is greatest at the central
wavelength
is greatest at the central
wavelength 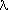 o, and
decreases as we shift from the core of the line to the wings. As the opacity
increases, we achieve a
o, and
decreases as we shift from the core of the line to the wings. As the opacity
increases, we achieve a  of
two-thirds for a shorter and shorter path length, and we see less far into the
medium (photons can travel less far before being absorbed, so those that
escape are emitted from the highest regions of the stellar atmosphere). The
line center thus come from higher (cooler) regions of the atmosphere, while
the profile wings come from deeper (hotter) zones.
of
two-thirds for a shorter and shorter path length, and we see less far into the
medium (photons can travel less far before being absorbed, so those that
escape are emitted from the highest regions of the stellar atmosphere). The
line center thus come from higher (cooler) regions of the atmosphere, while
the profile wings come from deeper (hotter) zones.
|
| [NMSU, N. Vogt] |
There are three primary mechanisms for line broadening:
natural,
Doppler, and
pressure (collisional) broadening.
For the H line in the solar
spectrum, natural broadening contributes 2 × 10-4 Angstroms,
Doppler broadening 0.4 Angstroms, and pressure broadening 1 ×
10-4 Angstroms.
line in the solar
spectrum, natural broadening contributes 2 × 10-4 Angstroms,
Doppler broadening 0.4 Angstroms, and pressure broadening 1 ×
10-4 Angstroms.
Natural broadening:
We apply Heisenberg's uncertainty principle to the uncertainty in the orbital
energy and the electron lifetime in an upper level.
Doppler broadening:
In thermal equilibrium, the atoms in a gas move randomly with a velocity
distribution which can be modeled as a Maxwell-Boltzmann function (between
v and v + dv for a mass m of atoms).
Pressure (collisional) broadening:
Electron orbitals can be perturbed by collisions with neutral atoms or by a
close encounter with the electric field of an atom. Individual collisions
combine to produce an overall collisional broadening in the line, with
pressure broadening based on the statistical sum of numerous close passes near
to ions. The effect scales with the time interval between encounters.
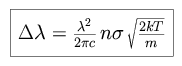 |
Remember that pressure broadening scales with n, the density of the
medium, and so can become much stronger in high density environments.
In low density environments, the line is optically thin and the equivalent
width EW is proportional to n. At intermediate values of n, the
core of the line saturates (becomes optically thick) but the wings remain
optically thin and can deepen (EW goes as the square root of log(n)).
For high densities, pressure broadening can deepen the wings and EW scales
with the square root of n.
For example, absorption features in luminous giant stars are narrow due to
their low atmospheric densities, while pressure broadening widens the lines in
denser Main Sequence star atmospheres where collisions are more common.

 is greatest at the central
wavelength
is greatest at the central
wavelength 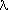 o, and
decreases as we shift from the core of the line to the wings. As the opacity
increases, we achieve a
o, and
decreases as we shift from the core of the line to the wings. As the opacity
increases, we achieve a  of
two-thirds for a shorter and shorter path length, and we see less far into the
medium (photons can travel less far before being absorbed, so those that
escape are emitted from the highest regions of the stellar atmosphere). The
line center thus come from higher (cooler) regions of the atmosphere, while
the profile wings come from deeper (hotter) zones.
of
two-thirds for a shorter and shorter path length, and we see less far into the
medium (photons can travel less far before being absorbed, so those that
escape are emitted from the highest regions of the stellar atmosphere). The
line center thus come from higher (cooler) regions of the atmosphere, while
the profile wings come from deeper (hotter) zones.

 line in the solar
spectrum, natural broadening contributes 2 × 10-4 Angstroms,
Doppler broadening 0.4 Angstroms, and pressure broadening 1 ×
10-4 Angstroms.
line in the solar
spectrum, natural broadening contributes 2 × 10-4 Angstroms,
Doppler broadening 0.4 Angstroms, and pressure broadening 1 ×
10-4 Angstroms.