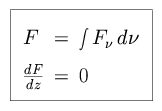
Energy transport in a planet's stratosphere, the region above the tropopause, is usually dominated by radiation. If the total radiative flux is independent of height, the atmosphere is said to be in radiative equilibrium. We consider the thermal profile for an atmosphere in radiative equilibrium, where, by definition, the total flux F is constant with depth.

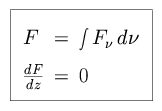The thermal structure, dT / dz, is governed primarily by the efficiency of energy transport, and depends strongly upon the opacity or optical depth. We can obtain the temperature structure from the diffusion equation, an expression for the radiative flux at height z. Here we will derive the diffusion equation for the case of an optically thick atmosphere which is in local thermodynamic equilibrium (i.e. I = S = B (T)), with monochromatic radiative equilibrium (dF / dz = 0, where F is the flux density across a layer in a stratified atmosphere). From the definition of the change in intensity through the atmosphere as a function of z, or of ,

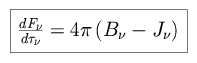Furthermore,

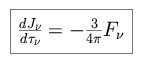We can set dF / d equal to zero, to find that

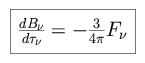We then integrate F over all frequencies to find the total radiative flux, arriving at the radiative diffusion equation.

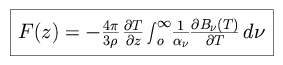We can simplify the form by defining _R, the Rosseland coefficient.

F then simplifies to the form

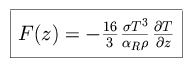The temperature profile is then

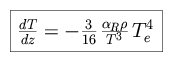Recall that flux travels upwards in an atmosphere if the temperature gradient dT / dz is negative (when temperature decreases with altitude). If the atmosphere is in both hydrostatic and radiative equilibrium, and its equation of state is given by the ideal gas law, then the temperature-pressure relation is simply

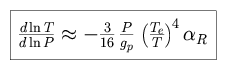When analyzing an atmosphere in radiative equilibirum, you may wish to divide the radiative flux into upwards and downwards components (the two-stream approximation).

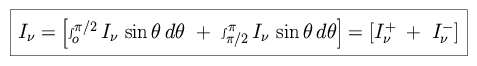The net flux density across an atmospheric layer can then be written as follows.
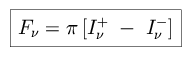