The specific intensity I is a conserved quantity, in the absence of sources or sinks of radiation (dI / ds = 0). Unless the light rays are traveling through a complete vacuum, however, energy will be added or removed by emission, absorption, and/or scattering.

We define the emission coefficient j as the amount of energy emitted per unit volume, per unit time, per unit frequency, into a solid angle (with units of ergs per second per cm³ per steradian per Hz).

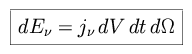Equating dV with dA × ds, the change in the specific intensity is thus

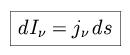If P is the power radiated per unit volume over all solid angles, for isotropic radiation P = 4 j.

We define the absorption coefficient as the change in specific intensity due to absorption. This process is stimulated directly by the incident flux, and so the amount of absorption scales with the specific intensity. We can visualize this by considering a medium which is composed of a number of discrete absorbers, scattered with a random distribution.

[NMSU, N. Vogt]

Our unit volume can be represented as a cylinder, with cross-sectional area dA and length dl. As the speed of light governs the amount of time that it takes for energy to pass along the cylinder, dl = c × dt. As long as the absorbers have a small enough characteristic projected area x that they do not overlap along a single ray passing along the cylinder, we can approximate the total absorbing volume for a ray passing through the cylinder as (n x) × dA ds. The amount of energy removed from the incident flux scales with this value.

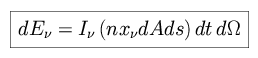thus

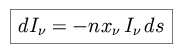and we define

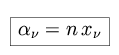such that
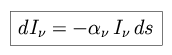