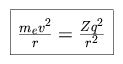
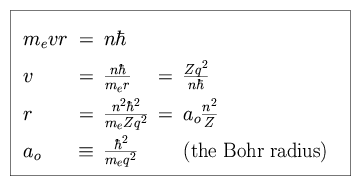
In the Bohr model of the atom, we balance the centripetal force with the Coulomb force. For an electron of charge -q, mass m_e (which we shall treat as equivalent to the reduced mass) and velocity v, in an orbit of radius r around a nucleus of atomic number Z,

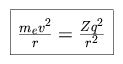The electron orbital paths are constrained such that the angular momenta are quantized, in units of 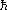( 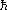= h / 2). Note that the principal quantum number n is the sum of the radial and the azimuthal quantum numbers (n = n_r + k). We can re-express this quantization as a constraint upon the orbital velocity v or radius r.

The energy of the n-th level orbit can be expressed as

When an electron makes a transition from state n to state m, a photon is emitted with an energy corresponding to the electron's change in energy.

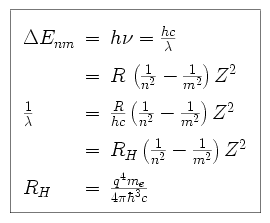This is the Balmer formula, which tells us the wavelengths of the discrete spectral lines emitted by atomic hydrogen. For n = 3, the Balmer formula gives a wavelength of 6563 Angstroms, the well-known H line. Other series have been found, most notably the Lyman, Paschen, and Brackett series, each describing different electron transitions of orbiting electrons in the hydrogen atom.

[NMSU, N. Vogt]