Introduction to Radiation
We define the energy and momentum of a photon as follows, where h is
Planck's constant, c is the speed of light,  is the frequency of the light, and
s is a unit vector which points in the direction of propagation.
is the frequency of the light, and
s is a unit vector which points in the direction of propagation.
We begin by considering the macroscopic properties of the radiation field.
In the absence of diffraction effects, radiation can be treated as traveling
in straight lines (rays). We consider the amount of energy dE which crosses
through an area s . dA, where  is the angle between the normal to
the surface area and s, into a solid angle d
is the angle between the normal to
the surface area and s, into a solid angle d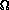 s in time dt with
frequency range d
s in time dt with
frequency range d .
.
 |
 |
| [NMSU, N. Vogt] |
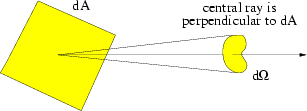
where
and the specific intensity I has units of
erg/s/cm2/str/Hz. Although I
has units of
erg/s/cm2/str/Hz. Although I is expressed as a scalar
quantity, it is defined as the intensity in a particular direction (along the
normal ray in the above diagram). The exception to this rule is the case of
an isotropic radiation field, for which the specific intensity is the
same in all directions. For a blackbody,
is expressed as a scalar
quantity, it is defined as the intensity in a particular direction (along the
normal ray in the above diagram). The exception to this rule is the case of
an isotropic radiation field, for which the specific intensity is the
same in all directions. For a blackbody,
The solid angle d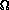 s
is defined so that, integrated over a sphere, it is equal to 4
s
is defined so that, integrated over a sphere, it is equal to 4 .
.
The mean intensity J is the zeroth moment of the
radiation field. This is the average of I
is the zeroth moment of the
radiation field. This is the average of I over all solid angles. For
isotropic radiation, J
over all solid angles. For
isotropic radiation, J =
I
=
I .
.
The energy density u is the amount of radiant energy
per unit volume at frequency
is the amount of radiant energy
per unit volume at frequency  .
Visualize a cylinder of side area dA and length c × dt, drawn around a set
of light rays traveling through d
.
Visualize a cylinder of side area dA and length c × dt, drawn around a set
of light rays traveling through d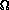 s. There is a certain
amount of energy within the cylinder. As the speed of propagation of light
(in a vacuum) is c,
s. There is a certain
amount of energy within the cylinder. As the speed of propagation of light
(in a vacuum) is c,
The net flux density F in the direction z at
frequency
in the direction z at
frequency  is the integral of
I
is the integral of
I cos
cos  over all solid angles. This is
equivalent to the net energy flow through the area dA into the solid
angle d
over all solid angles. This is
equivalent to the net energy flow through the area dA into the solid
angle d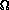 s. For an
isotropic radiation field, the net energy flow is zero.
s. For an
isotropic radiation field, the net energy flow is zero.
We define H as the
first moment of the intensity I
as the
first moment of the intensity I .
.
The second moment K is then
is then
which is related to the radiation pressure pr as follows.
The momentum flux, integrated over all frequencies along the direction
s is equal to dF/c. The radiation pressure is simply the component of
the momentum flux in the z direction.
 is the frequency of the light, and
s is a unit vector which points in the direction of propagation.
is the frequency of the light, and
s is a unit vector which points in the direction of propagation.
 is the frequency of the light, and
s is a unit vector which points in the direction of propagation.
is the frequency of the light, and
s is a unit vector which points in the direction of propagation.

 is the angle between the normal to
the surface area and s, into a solid angle d
is the angle between the normal to
the surface area and s, into a solid angle d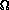 s in time dt with
frequency range d
s in time dt with
frequency range d .
.




 has units of
erg/s/cm2/str/Hz. Although I
has units of
erg/s/cm2/str/Hz. Although I is expressed as a scalar
quantity, it is defined as the intensity in a particular direction (along the
normal ray in the above diagram). The exception to this rule is the case of
an isotropic radiation field, for which the specific intensity is the
same in all directions. For a blackbody,
is expressed as a scalar
quantity, it is defined as the intensity in a particular direction (along the
normal ray in the above diagram). The exception to this rule is the case of
an isotropic radiation field, for which the specific intensity is the
same in all directions. For a blackbody,

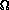 s
is defined so that, integrated over a sphere, it is equal to 4
s
is defined so that, integrated over a sphere, it is equal to 4 .
.

 is the zeroth moment of the
radiation field. This is the average of I
is the zeroth moment of the
radiation field. This is the average of I over all solid angles. For
isotropic radiation, J
over all solid angles. For
isotropic radiation, J =
I
=
I .
.

 is the amount of radiant energy
per unit volume at frequency
is the amount of radiant energy
per unit volume at frequency  .
Visualize a cylinder of side area dA and length c × dt, drawn around a set
of light rays traveling through d
.
Visualize a cylinder of side area dA and length c × dt, drawn around a set
of light rays traveling through d s. There is a certain
amount of energy within the cylinder. As the speed of propagation of light
(in a vacuum) is c,
s. There is a certain
amount of energy within the cylinder. As the speed of propagation of light
(in a vacuum) is c,

 in the direction z at
frequency
in the direction z at
frequency  is the integral of
I
is the integral of
I cos
cos  over all solid angles. This is
equivalent to the net energy flow through the area dA into the solid
angle d
over all solid angles. This is
equivalent to the net energy flow through the area dA into the solid
angle d s. For an
isotropic radiation field, the net energy flow is zero.
s. For an
isotropic radiation field, the net energy flow is zero.

 as the
first moment of the intensity I
as the
first moment of the intensity I .
.

 is then
is then

