We consider next a constrained aspect of the three body central force problem - the restricted, circular three body problem. By restricted we mean that one of the three bodies has a negligible mass in comparison to the other two. Consider the case of two massive bodies, moving in circular orbits about their center of mass. We introduce a third body of negligible mass, which has no significant effect on the orbits of the two massive bodies. For convenience, we shall work in a non-inertial frame of reference which rotates about the center of mass at a rate equal to the orbital frequency of the two massive bodies.
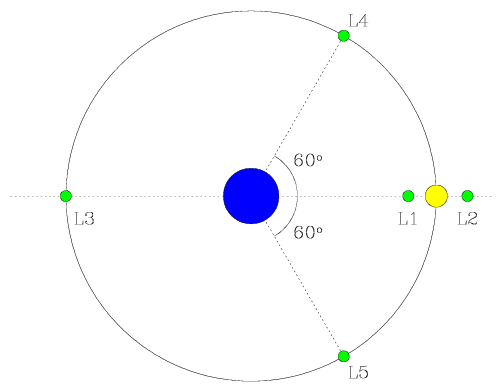
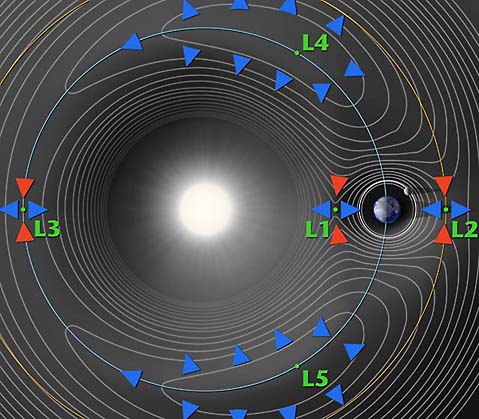
Lagrange showed that there are five points in such a system where a test particle, placed at rest, would feel no net force in the rotating non-inertial frame. Three of these points (L1 through L3) lie along the line which runs through the two massive bodies. The remaining points (L4 and L5) form equilateral triangles with the two massive bodies, as we shall show as part of Homework #5.
|
| [NMSU, N. Vogt] |
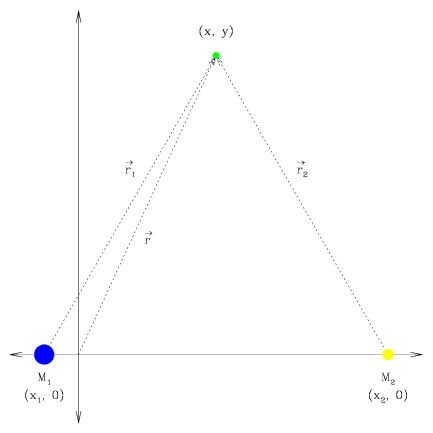
We begin by placing the zeropoint of our coordinate system at the center of mass of the system, and define the x-axis as the line which runs through the two massive bodies.
 |
| [NMSU, N. Vogt] |
We can now evaluate the potential at position (x, y).
 |
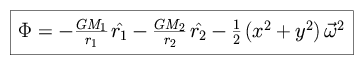where 
, the orbital frequency of
the reference frame, is determined from Kepler's Third Law.
 |
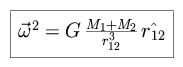We take partial derivatives along both axes, setting them equal to zero at the points of equilibrium.
 |
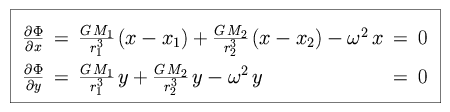For the case y = 0 (i.e. r = x), the partial derivative with respect to x yields three Lagrange points located along the x-axis. For the case of non-zero y, the partial derivative with respect to y can be expressed as follows.
 |
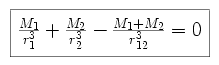We can then use the fact that M1 x1 = - M2 x2 to prove that the remaining two Lagrange points lie 60 degrees off of the x-axis (i.e. |r1| = |r12| = |r2| for L4 and L5).
A contour map shows the effective potential around the Sun-Earth Lagrange points. L4 and L5 correspond to hilltops and L1, L2 and L3 correspond to saddles (i.e. points where the potential is curving up in one direction and down in the other).
 |
| [NASA/GSFC] |