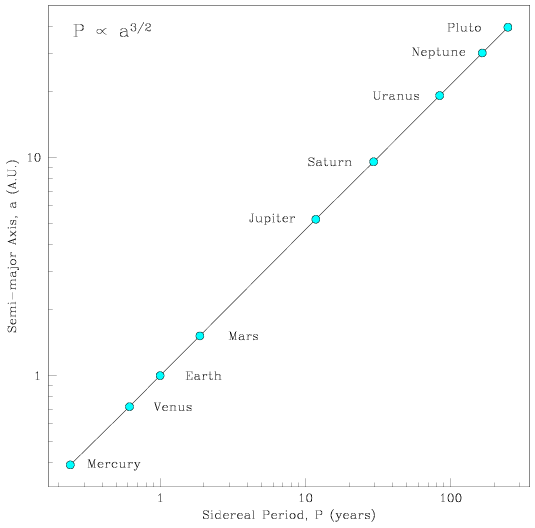
The squares of the sidereal periods of the planets are proportional to the cubes of the semi-major axes of their orbits.
The semi-major axis of a planet is equal to the mean distance of the planet, so one can also say that the cube of the mean distance of a planet is proportional to the square of its sidereal period.
 |
| [NMSU, N. Vogt] |
If a1 and T1 refer to the semi-major axis and sidereal period of a planet P1 moving about the Sun,
the constant being the same for any of the planetary orbits. If a2, a3,..., and T2, T3, ..., refer to the semi-major axes and sidereal periods of the other planets P2, P3, ..., moving about the Sun, then
The most convenient form for the constant is obtained by taking the planet to be the Earth and expressing the distance in astronomical units and the time in years. Hence, for the Earth, a = 1 and T = 1, so the constant becomes unity. For any other planet, consequently,
showing that if we measure the sidereal period, T, of a planet in Earth-years, we can obtain its mean distance from the Sun, a, in AU. Kepler showed that the four moons of Jupiter discovered by Galileo also obeyed his third law, though with a different value of the constant, confirming its wide applicability. The so-called constant in Kepler's third law is actually dependent on the masses of the two celestial bodies in orbit about each other. Nevertheless, when one of the bodies is significantly more massive that the other, such as the Sun compared to the planets, or Jupiter compared to its satellites, Kepler's third law is a very close approximation to the truth. Only when the outer-most retrograde satellites in the solar system are considered, or close satellites of a non-spherical planet, do Kepler's laws fail to describe the behavior of such bodies with significant precision.
This is simply a specific case of the general relation between semi-major axis a and orbital period P for a point mass in orbit around a mass M, governed by the gravitational force.
 2 =
a3 / P2
2 =
a3 / P2