Clocks
Sidereal Time:
The rotation of the Earth causes a regular change in the apparent
positions of stars, so the hour angle of a star can be used as a measure of
time. We use the hour angle of the first point of Aries, HA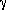 , as a measure of the rotation of the
Earth with respect to the stars. This is known as local sidereal time:
, as a measure of the rotation of the
Earth with respect to the stars. This is known as local sidereal time:
LST = HA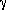
and is zero when the first point of Aries crosses the observer's meridian.
As its name implies, local sidereal time depends upon the observer's longitude
on the Earth's surface. The HA is equal to the sum of the right ascension of
the star X (RAX) and the hour angle of the star X (HAX). Hence,
LST = RAX + HAX.
This is a very important relationship because X can be any celestial object
- star, Sun, Moon, planet or spacecraft. Since the hour angle of a star is
zero when it transits on the observer's meridian, the star's right ascension
at that time is the local sidereal time (or, equivalently, the local sidereal
time gives the right ascension of the star).
Solar Time:
Civil time keeping is based on the hour angle of the Sun (HAS) instead of
the hour angle of the first point of Aries. This is known as apparent solar
time (AST):
AST = HAS
and is zero when the Sun crosses the observer's meridian. An apparent
solar day is defined as the time interval between successive passages of the
Sun across the observers' meridian. The time it takes the Sun to return to the
same point in the sky each day is slightly longer than one sidereal day, which
is the time it takes the stars to return to the same point in the sky each
night.
 |
| [NMSU, N. Vogt] |
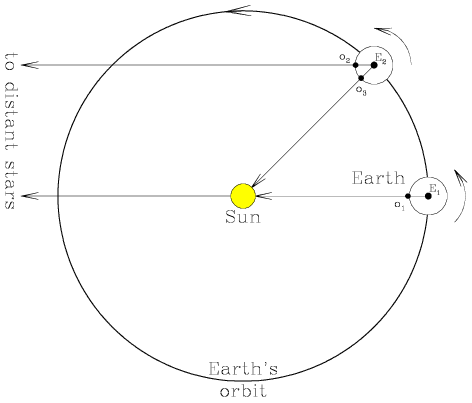
An observer at O1 on the surface of the Earth observes the Sun
and a star on the meridian. Taking the distance of the star to be effectively
infinite compared to the Sun, the observer will next observe the star to
transit at O2 when the Earth has rotated once on its axis.
However, in the time the Earth has taken to rotate once on its axis, it has
also moved in its orbit around the Sun by 360/365.25=0.99°, from position
E1 to E2. The Earth will thus have to rotate on its axis
until the observer is at O3 for the Sun to appear again on the
meridian. The apparent solar day is therefore longer than the sidereal day by
a time interval equal to the time it takes the Earth to rotate on its axis by
the angle 360°/365.25, i.e. approximately four minutes. Given that an
apparent solar day is 24 solar hours in length, this means that a sidereal day
is only 23h56m long in solar units and represents the
rotational period of the Earth. Another way of expressing this is that the Sun
appears to move backwards through the stars by four minutes (or 1°) each
day.
Each type of day (apparent solar and sidereal) can be divided into hours,
minutes and seconds, but the solar version of each is
24h/23h56m = 1.0028 times or 0.28% longer
than the sidereal equivalent.
Universal Time:
The hour angle of the sun depends on the location of the observer and
varies with longitude. It is therefore more convenient and less ambiguous to
refer to a standard longitude, which was chosen by international agreement in
1884 to be the longitude of the old Royal Observatory at Greenwich. We can
then define Greenwich mean time (GMT), or universal time, in terms of
the hour angle of the sun at Greenwich (GHAMS):
UT = GMT = GHAMS +/- 12h
where the plus or minus sign is used if the GHAMS is less than or greater
than 12h, respectively, in order to make the UT 0h at
midnight. For convenience, time within a particular country or geographical
region is defined by time zones, 15° wide in longitude, within each of
which the time is the same (the mean solar time at the center of the
zone). The standard time or zone time is then defined by:
ST = ZT = UT + n
where n is given in hours and is a constant for a particular time
zone, being negative for western longitudes and positive for eastern ones:
n = (longitude in degrees at center of zone) / 15
In most cases n is taken to be an integer, so that different time
zones are an exact number of hours apart. An exception is India, where
n=5.5. For geographical reasons, the time-zone borders do not always
follow lines of longitude; for example, the International Date Line, which
marks the center of the zones +/-12, snakes its way around groups of Pacific
islands so that all islands in a group agree on the date.
Before the advent of accurate clocks, the rotation of the Earth was the
fundamental time keeper for all purposes, both astronomical and civil. As soon
as clocks became precise enough to detect fluctuations in the rotation rate of
the Earth, the importance of astronomical observations for civil time keeping
began to diminish and nowadays intervals of time are defined by atomic clocks,
the corresponding time scale being known as coordinated universal
time. This drifts slowly with respect to UT, because of fluctuations in
the Earth's rotation rate, and leap seconds are added from time to time to
keep UTC in phase with UT. Otherwise, (civil) noon would eventually be at
(astronomical) midnight. Thus we still rely on astronomical observations to
keep the zero-point of our timescales correct.
Ephemeris Time:
Visualize the planar surface in which Jupiter's orbit lies. We can
measure the moment at which the Earth crosses this plane, twice per orbit, and
define a unit of ephemeral time as the interval between successive crossings
in the same direction (e.g. successive breaking of the plane from below, or
successive breaking of the plane from above).
Atomic Time:
Consider the cesium isotope 133Cs, which has a ground state
transition between two hyperfine levels. We can measure the frequency of the
radiation emitted during this transition, and the period of this radio wave
serves as a unit of atomic time.
Nuclear Time:
We know that 3H will beta decay into 3He. If the
tritium is cooled to 10 K, the helium will diffuse outward as it forms. When
the mass of the tritium sample drops to half of its initial value, one unit of
nuclear time has elapsed.
Pulsar Time:
There exist binary pulsars which emit signals with a periodicity,
resulting from the neutron star rotation, which varies by less than one part
in ten billion per year.
We can measure time by tracking inertial processes (the Earth's rotational
rate), gravitational force (orbital patterns), electromagnetic processes, or
nuclear beta decay (weak force) and alpha decay (strong force). Universal and
ephemeral time should be related, if general relativity holds; should we
assume that the time measured by all of these processes is equivalent?
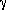 , as a measure of the rotation of the
Earth with respect to the stars. This is known as local sidereal time:
, as a measure of the rotation of the
Earth with respect to the stars. This is known as local sidereal time:
