[NMSU, N. Vogt]

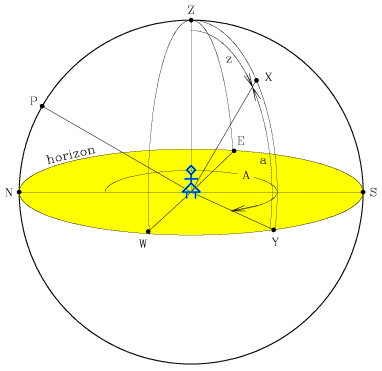
The alt-az (horizontal) coordinate system is the simplest coordinate system, as it is based on the observer's horizon. The celestial hemisphere viewed by an observer on the Earth is shown above. The great circle through the zenith Z and the north celestial pole P cuts the horizon NESYW at the north point (N) and the south point (S). The great circle WZE at right angles to the great circle NPZS cuts the horizon at the west point (W) and the east point (E). The arcs ZN, ZW, ZY, etc, are known as verticals.

The two numbers which specify the position of a star, X, in this system are the azimuth, A, and the altitude, a. The altitude of X is the angle measured along the vertical circle through X from the horizon at Y to X. It is measured in degrees. (An often-used alternative to altitude is the zenith distance, z, of X, indicated by ZX. Clearly, z = 90 - a.) Azimuth is defined as the angle between the vertical through the north point and the vertical through the star at X, measured eastwards from the north point along the horizon from 0° to 360°. This definition applies to observers in both the northern and the southern hemispheres.

The main advantages of the alt-az system are that it indicates clearly how high a star is above the horizon and in what direction it can be found. The main disadvantage is that it is a local coordinate system, so two observers at different points on the Earth's surface will measure different altitudes and azimuths for the same star at the same time. In addition, a star's alt-az coordinates change with time as the celestial sphere appears to rotate. Despite these problems, most modern research telescopes use alt-az mounts, owing to their low cost and great stability.