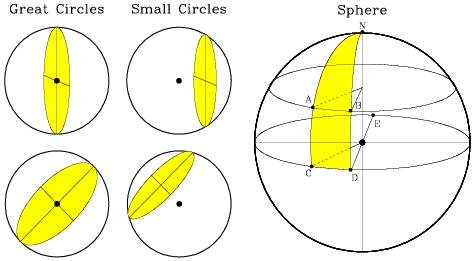
A great circle is defined as the intersection between the surface of a sphere and a plane containing the center of the sphere. If the plane does not contain the center of the sphere, though all points within the intersection of the sphere and the plane are equidistant from the center of the sphere, the intersection is termed a small circle. (The radii of all small circles on a given sphere are always less than that of the great circles.) The shortest path between two points on the surface of a sphere is given by the arc of the great circle passing between them.
To connect three points on the surface of a sphere using the shortest possible path, we would draw arcs of great circles and create a spherical triangle. A triangle drawn on the surface of a sphere is a spherical triangle if it has all of the following properties:
On the sphere pictured below, triangle NAB is not a spherical triangle (as the side AB is an arc of a small circle), but triangle NCD is a spherical triangle. You can see that the above definition of a spherical triangle also rules out the "conjugate triangle" NCED as a spherical triangle, as the vertex angle N is greater than 180° and the sum of the sides NC and ND is less than CED.
 |
| [NMSU, N. Vogt] |
Please note that in a true linear representation of the sphere, we could not portray both the equatorial great circle upon which points E, C, and D fall as an ellipse (at not quite edge-on orientation), and simultaneously portray a polar great circle (containing point N, and unlabeled counterpoint S) as lying along the outer circumference of the drawn sphere (at face-on orientation, rather than having N tipped toward the observer and S tipped away from the observer), from a single viewing position. We employ a slightly non-linear (warped) representation, having found that students tend to instinctively interpret the diagrams correctly and make a mental adjustment to compensate for the two viewing angles, and because a strict linear form of the diagram can be more confusing and adds yet more complexity to the design process.
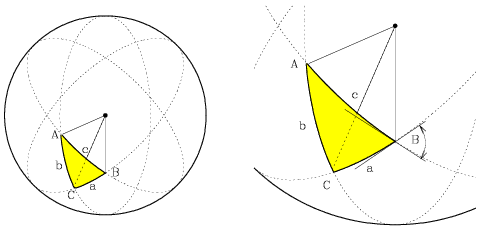
The next figure shows a spherical triangle, formed by three intersecting great circles, with arcs of length (a,b,c) and vertex angles of (A,B,C). Note that the angle between two sides of a spherical triangle is defined as the angle between the tangents to the two great circle arcs, as shown on the right for vertex angle B. The arc lengths (a,b,c) and vertex angles (A,B,C) are related as follows.
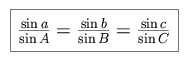 |
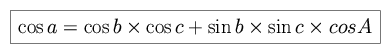 |
 |
| [NMSU, N. Vogt] |
Thanks to Vik Dhillon for the base contents of this material on spherical mechanics.