Consider the case of light being diffracted through a single slit, where the wavelength 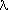is much larger than the slit width d.

[NMSU, N. Vogt]

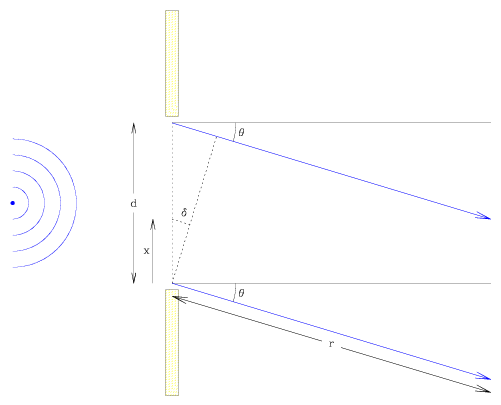
The contribution to the total flux from a small length dx at a position x along the slit will be offset in phase by 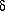= x sin from the flux at the lower edge of the slit, and can be expressed as

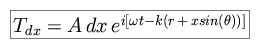The total flux across the entire slit is just a combination of such elements.

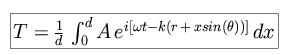and we can use Euler's formula and small angle approximation to reduce this to

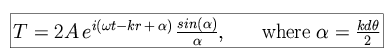The intensity of the light is then

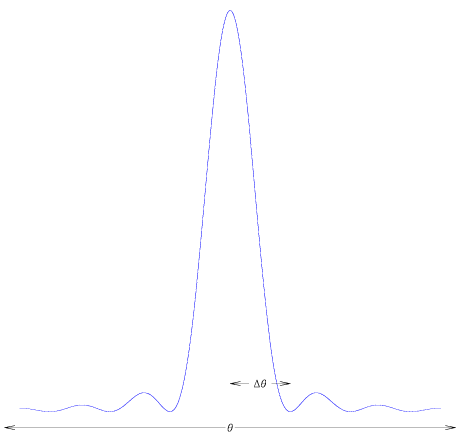
If we place a screen a distance f away from the slits, then we will observe the following pattern. The first minimum will appear a distance of = f 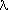/ d along the screen.

[NMSU, N. Vogt]

We can use this to determine the diffraction limit for a telescope. To first order, we simply replace the slit width d in the above derivation with the diameter of the telescope, and determine the smallest angular separation on the sky across which two point sources can be resolved. (Two point sources of the same wavelength are just resolved if the maximum intensity of one occurs at the position of the first diffraction minimum of the second.) We can define the limit as L, where

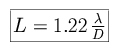The factor of 1.22 is due to the fact that the telescope mirror is a circular aperture, rather than an infinite slit. The diffraction limit for even a four inch objective is an arcsecond. Compare this to the size of the seeing disk at various observatories!

• What is the diffraction limit of an optical telescope?
• What is the diffraction limit of a radio telescope?
• What is the diffraction limit of an interferometric array of radio telescopes?