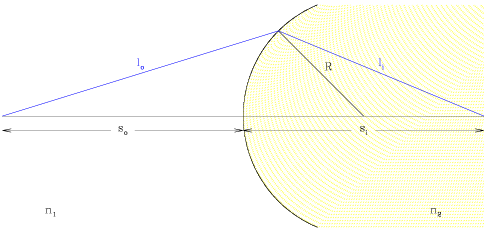
We begin by deriving the relationship between between the path of incident and refracted light from an initial medium of index of refraction n₁ through a spherical surface with radius of curvature R and index of refraction n₂.

[NMSU, N. Vogt]

We first define the effective optical path length, the distance that a light ray travels through both media.

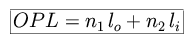Fermat's principle tell us that the optical path length is stationary with respect to the position variable (in this case, the location of the interface point along the surface of refraction). The position variable is constrained by , the angle between a radial chord pointing from the center of the sphere to the interface point, and the optical axis.

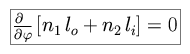We use the law of cosines to define l in terms of s, R and , and determine that

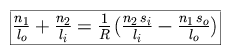We can now focus our attention upon the paraxial region, near to the optical axis, in which incoming rays are effectively parallel to the optical axis . For such small values of 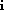, we can use the small angle approximation and our equation simplifies to the form

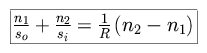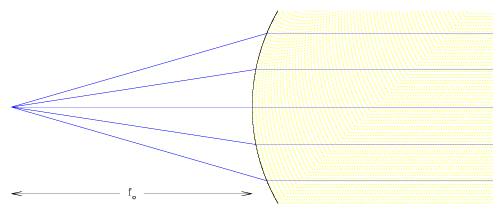
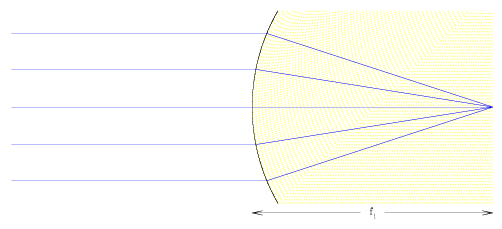
We define the object focus f_o as the point which is imaged at infinity when refracted and focused through the sphere,

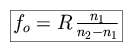[NMSU, N. Vogt]

and the partner image focus f_i as the point at which an object from infinity is focused through the sphere

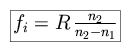[NMSU, N. Vogt]

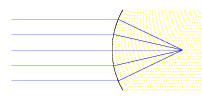
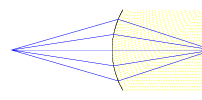
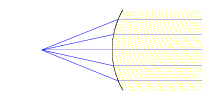
We can evaluate four cases of objects imaged through the spherical surface, by varying the object position along the optical axis.

• The object is effectively at a distance of infinity, and the image is focused at the image focus f_i.
• The object is placed closer to the surface, and the image is focused beyond f_i.
• The object is placed at the object focus f_o, and the image is focused at infinity.
• The object is placed closer to the surface than f_o, and a virtual image appears outside of the surface (s_i < 0).

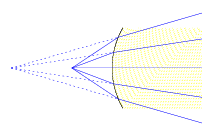[NMSU, N. Vogt]