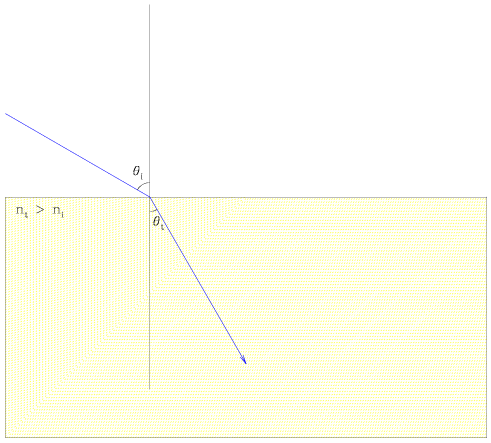
Light can refract through a surface. When light encounters a discontinuity in the medium through which it is being transmitted, a fraction of the light will be reflected away from the plane and the remaining portion will be transmitted (refracted) through the new medium. We define the angle of incidence and the angle of refraction relative to the normal with respect to the plane of discontinuity. With some thought, we can find the relationship between these angles just as we did in the case of the reflected wave.

[NMSU, N. Vogt]

A good example of this phenomenon is the simple case of a drinking straw placed in a glass of water, which appears to bend and change width as it enters the water.

Less commonplace, but slightly more exciting, is the case of the goldfish which does not lie at the location at which it appears when spotted from the air.

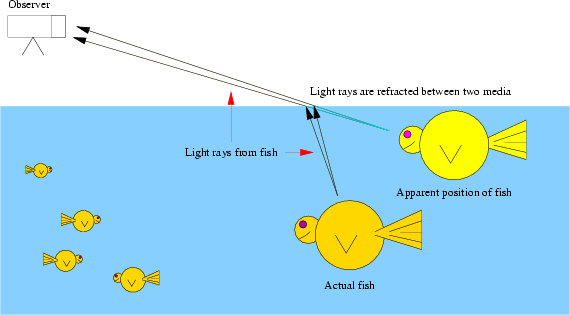[NMSU, N. Vogt]

Less simple, but slightly more intriguing, is this image of glassware demostrating both reflection and refraction from multiple surfaces. This is a good example of the sort of image that you can construct with POVRAY, given semi-infinite amounts of time.

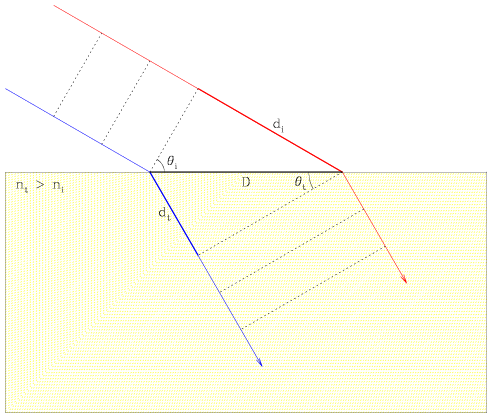
Consider the case of light being emitted from a distant source and impacting upon a plane. Two parallel rays of light (blue and red lines) are emitted such that successive wavefronts are in phase, remain in phase as they travel towards the plane, and will be in phase after they are transmitted into the plane. The incident red ray of light travels an extra distance d_i more than the blue ray before entering the second medium, and the blue ray travels an extra distance d_t more than the red ray afterward. The dashed lines represent successive wavefronts, the elements of which are by definition in phase before and after transmission. (A set of congruent light rays will preserve the state of congruence with respect to an arbitrary number of refractions.) We can use this phasing requirement to constrain the reflection of both rays of light.

We have an added complication, however. Because we are considering the transmission of light through more than one medium, we need to account for the variation in the speed of light through each medium as a function of the atomic lattice structure. We define the index of refraction, n, such that

Velocity (v) = c / n

and use this phasing requirement to constrain the transmission of both rays of light.

Velocity (v) = Distance (d) / Time (t) = c / n

ti = tt

di = D sin(i)

dt = D sin(t)

c = n d / t

ni sin(i) = nt sin(t)

The angle of transmission is related to the angle of incidence through the ratio of the absolute indices of refraction, or the relative index of refraction.

[NMSU, N. Vogt]

Medium	n	Medium	n
Vacuum	1.00	Quartz crystal	1.54
Air	1.00	Salt	1.54
Ice	1.31	Emerald	1.57
Water	1.33	Carbon Disulfide	1.63
Glycerin	1.47	Heavy Flint Glass	1.65
Crown glass	1.52	Heaviest Flint Glass	1.89
Zinc Crown Glass	1.52	Diamond	2.42