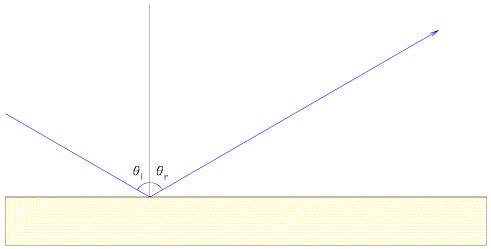
Light can reflect off of a surface. When light encounters a discontinuity in the medium through which it is being transmitted, a fraction will be reflected. We define the angle of incidence and the angle of reflection relative to the normal with respect to the plane of discontinuity. With some thought, we can find the relationship between these angles. A good example of this phenomenon is the simple of case of light reflecting off of a mirror.

[NMSU, N. Vogt]

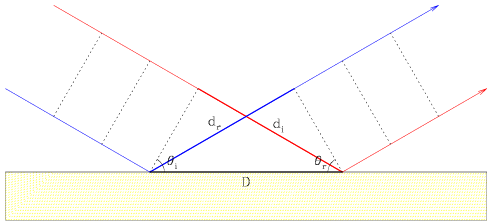
Consider the case of light being emitted from a distant source and impacting upon a plane. Two parallel rays of light (blue and red lines) are emitted such that successive wavefronts are in phase, remain in phase as they travel towards the plane, and will be in phase after they reflect off of the plane. (We confirm this result every morning when we manage to comb our hair in the mirror.) The incident red ray of light travels an extra distance d_i more than the blue ray before reflecting, and the blue ray travels an extra distance d_r more than the red ray after reflecting. The dashed lines represent successive wavefronts, the elements of which are by definition in phase, before and after reflectance. We can use this phasing requirement to constrain the reflection of both rays of light.

Velocity (v) = Distance (d) / Time (t) = c

ti = tr

di = D sin(i)

dr = D sin(r)

i = r

The angle of reflection is equal to the angle of incidence.

[NMSU, N. Vogt]