- Johannes Kepler (1571 – 1630) was a mathematician and astronomer who lived in one of the small northern principalities of the Holy Roman Empire. He worked with Tycho Brahe to understand the movements of the planets and the stars in the heavens. We remember him primarily for his three laws of planetary motion (details, with diagrams) :
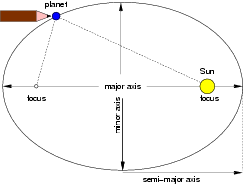
- The planets orbit the Sun in elliptical paths, with the Sun located at one focal point
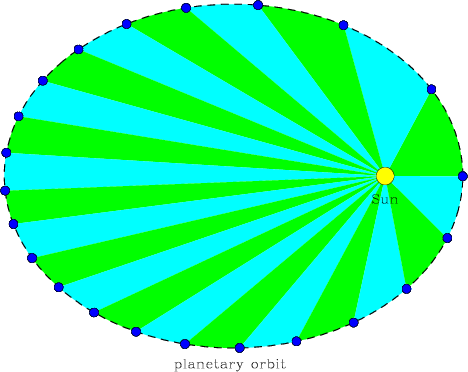
[NMSU, N. Vogt] - A line drawn from a planet to the Sun will sweep over equal areas in equal amounts of time
[NMSU, N. Vogt] - The square (second power) of the period of a planet is directly proportional to the cube (third power) of its orbital radius (P2 = R3). This is because the closer a planet lies to the Sun, the faster it must spin to resist the gravitational attraction (and to avoid falling into the Sun).
Planet Period P Orbital Radius R P2 / R3 (years) (A.U.) (yr2 / A.U.3) Mercury 0.241 0.39 0.98 Venus 0.615 0.72 1.01 Earth 1.00 1.00 1.00 Mars 1.88 1.52 1.01 Jupiter 11.8 5.20 0.99 Saturn 29.5 9.54 1.00 Uranus 84.0 19.18 1.00 Neptune 165 30.06 1.00 Pluto 248 39.44 1.00 When we plot the planetary radii against their periods, we see that they fall on a straight line. If we know how far a planet lies from the Sun, we can determine the length of its year. Likewise, if we know how long it takes for a planet to orbit the Sun, we can determine its orbital radius.
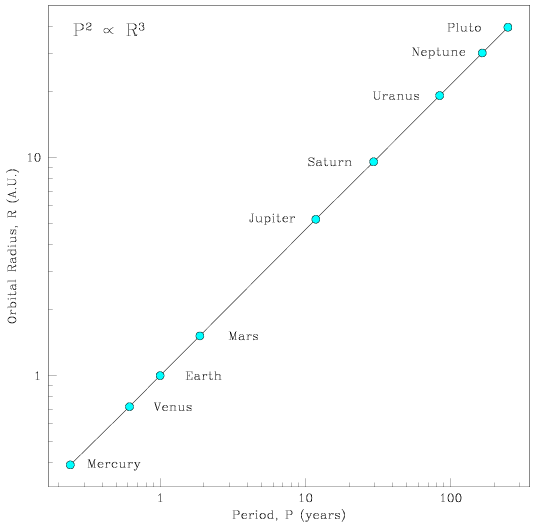
[NMSU, N. Vogt] - The square (second power) of the period of a planet is directly proportional to the cube (third power) of its orbital radius (P2 = R3). This is because the closer a planet lies to the Sun, the faster it must spin to resist the gravitational attraction (and to avoid falling into the Sun).