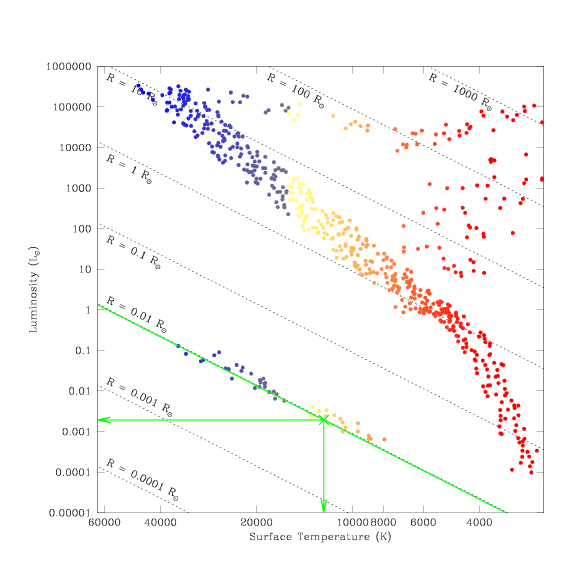
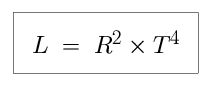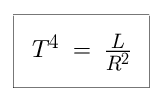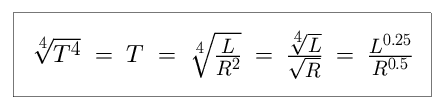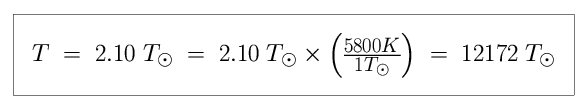What kind of stars are found here?

A star in this region of the Hertzsprung-Russell diagram has a temperature of roughly 12,000 Kelvin (12,000 K), a luminosity 500 times less than that of the Sun (0.002 × L), and a radius one hundred times smaller than the Sun (R = 0.01 × R). This star lies along the narrow band in size, where white dwarf stars are found. The fairly low temperature indicates that this star is the end-product of a nova of a low-mass star that took place some time in the past (a younger star would not have had time to cool, and to move down the white dwarf sequence to such lower luminosities and cooler temperatures).

Try to read the values of L, T, and R for yourself from the diagram. Do you estimate values for the luminosity, temperature, and size of the star similar to those listed above?

How can we find the temperature T of a white dwarf in this region of the Hertzsprung-Russell diagram, if we know its luminosity L?

We can use the Stephan-Boltzmann Law to relate the temperature (T), size (R), and luminosity (L) of a star to each other. Measuring L, R, and T in solar units, we say that:

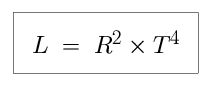Our next step is to solve for T in this equation. Dividing through by R squared, we see that

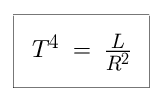We now take the fourth root of both sides of the equation, in order to find an expression for T. T is equal to the fourth root of L, divided by the square root of R.

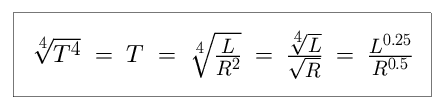
Let us say that the luminosity of the star is exactly 0.00194 times that of the Sun, and the radius is roughly 0.01 in solar units, as the Hertzsprung-Russell diagram shows us that all white dwarfs are roughly one-hundredth of the size of the Sun. We can use these values to find the temperature, in units of the temperature of the Sun.

This white dwarf is almost three times hotter than the Sun. Now, we can convert this value into degrees, as we know that the Sun has a surface temperature of 5800 K.

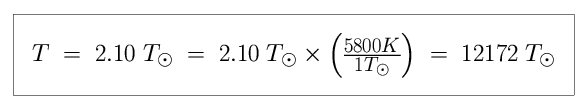
We estimated a value of T = 12,000 K from the diagram, for stars found in this area – a reasonable value!