The dilemma of a bright sky at night for a static, uniform density,
infinite universe is known as Olbers' paradox, after Heinrich Olbers who posed
the question of why the sky is dark at night in 1826. The problem was
actually pointed out before this by J. P. L. de Chesaux, a Swiss astronomer, in 1744, and addressed by
a diverse group of scholars ranging from Lord Kelvin to Mark
Twain and Edgar Allen Poe.
Suppose that the Universe is static, infinite in size, and of constant density.
- Show that the night sky would not be dark (the flux density observed at the Earth is infinite).
For a star of average luminosity L, the apparent flux from the star,
observed from the Earth, is
For a spherical shell of radius r and width dr, the
apparent flux, observed from the Earth, is
Integrating over the set of shells which make up an infinite sphere
surrounding the Earth, we find the total flux.
- Could this dilemma be overcome by invoking extinction? Why, or why not?
We begin by assuming that extinction is caused by a constant density field
which permeates the entire Universe, and modify our equations for flux accordingly.
Invoking extinction does appear to prevent the observed flux from diverging
to infinity. However, the absorbing medium cannot act as an unlimited light
sink indefinitely. It will re-emit the absorbed energy, thus re-introducing
the light back into the total observed flux. In the case of our static
Universe, even small accumulations of heat and light would sum to a significant
amount of flux. Thus, re-emission, even at longer wavelengths, will serve to
rejuvenate the total flux.
Now suppose that the Universe is expanding, and follows Hubble's Law (v = Ho r).
- Show that the flux density observed at the Earth is no longer infinite
We begin by calculating the average distance along a line of sight to a star.
The percentage P of the sky which is filled with stars, within a given
shell, is as follows, where the radius of the star with luminosity L is
defined as R.
We require that the sky filling factor be be normalized as follows.
We then solve for the average distance along a given line of sight to a
star, assuming that the average solar radius R is that of the Sun (7
× 10
 cm), and the density of stars
no is roughly 10
cm), and the density of stars
no is roughly 10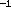
 per cubic light-year.
per cubic light-year.
We can now recalculate the total flux observed at the Earth.
While no longer infinitely bright, the night sky should still be as bright
as the noonday Sun. Note, however, that Rav >> Rev,
where Rev is the event horizon of standard Universe expansion
models. The sky may thus be dark at night because all lines of sight do not
intersect with a star which lies within our event horizon, the portion
of the Universe across which light has had time to travel towards us over the
age of the Universe.
We proceed to assume an expansion rate of the form
where Ho is the Hubble constant, measured in units of kilometers
per second per megaparsec, and is roughly equal to 75. The observed flux from
a star of luminosity L a distance r from Earth is now affected
by cosmological dimming. This causes the introduction of two factors of (1 +
z) in the denominator: one for pure time dilation, and one caused by
the redshifting of the emitted light.
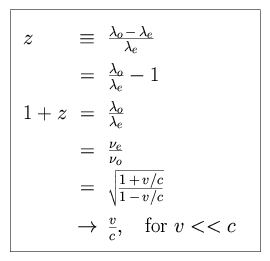
We now need to restate (1 + z) in terms of the distance r to
the star. Recall that z is simply the shift in wavelength, or
frequency, observed in a particular spectral feature. Recalling the effect of
time dilation upon the emission of light at a characteristic frequency,
We can now introduce this form for (1 + z) into our expression for
fL, and calculate the observed flux accordingly.
We require that v be less than or equal to the speed of light,
i.e. that r be less than or equal to c / Ho. This sets a
maximum limit on the spatial extent of our (formerly infinite) sphere of
shells. Using the change of variable  =
r + c / Ho,
=
r + c / Ho,
This is a far more realistic answer!
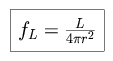
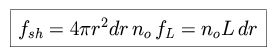
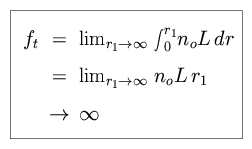
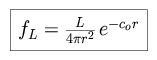
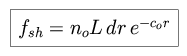
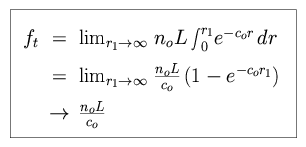
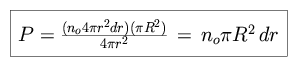


 cm), and the density of stars
no is roughly 10
cm), and the density of stars
no is roughly 10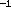
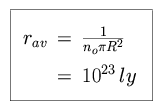
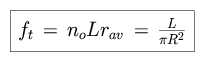
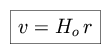
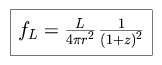
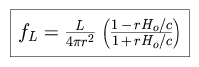
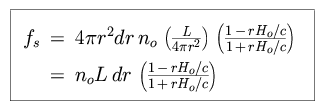
 =
r + c / Ho,
=
r + c / Ho,
