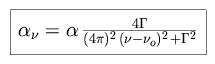
The shape of spectral features, namely emission and absorption lines, is determined by the abundance of various elements or compounds and the pressure and temperature of the environment. Spectral data can thus be used to determine abundances, the distribution of species with depth, and the thermal structure of a medium. They can also be used to recover the velocity distribution (kinematics), in the form of winds (atmospheres), or orbital motions (stars).

Lorentz Profiles (Natural damping):
Emission and absorption features always display a finite width, the natural damping profile widened by the effects of motion and by observational effects (seeing conditions, resolution of equipment). The narrowest profile a line can exhibit, under optimum observing conditions, is a function of the finite lifetime of the excited atomic states within the medium. The shape of this profile can be characterized by the Lorentz line shape.

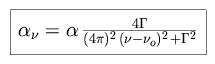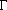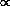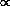where is the reciprocal of the lifetime of all states giving rise to emission or absorption at frequency ( 1/t 1/). , _o is the central frequency, and is the spectrally integrated extinction coefficient (where f_osc is the oscillator strength).

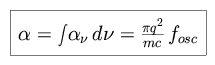Voigt Profiles (Doppler broadening):
When an atom travels with a velocity v_r along the line of sight, the frequency of its absorption and emission is shifted in frequency space by the amount

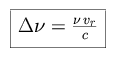This shift is positive (blue, towards higher frequencies and shorter wavelengths) if the atom is moving towards the observer, and negative (red, towards lower frequencies and longer wavelengths) if the atom is moving away from the observer. In an atmosphere, the atoms and molecules move in all directions and the radial velocity can be expressed with a Maxwellian distribution. The net effect is a broadening of the line profiles, and the shape of a broadened profile can be modeled by convolving the underlying Lorentz profile with the Maxwellian velocity distribution.

The probability of finding an atom with a radial velocity between v_r and v_r + dv_r can be expressed as follows.

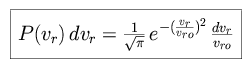where

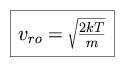and the product in the denominator is the molecular mass. The absorption profile can then be written as follows.

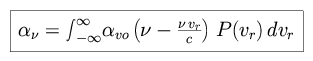which results in the Voigt profile for absorption.

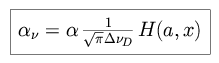with the Doppler width _D.

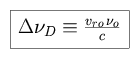The Doppler width is the full width of the line at half maximum (FWHM), divided by a normalizing factor. The Voigt function is defined as follows.

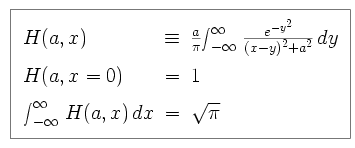where

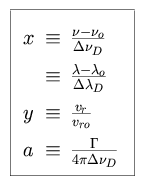When Doppler broadening dominates a profile, the Voigt profile can be expressed as the following.

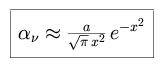Pressure or collisional broadening:
In a dense gas, collisions between particles dominate and perturb the energy levels of the electrons sufficiently that photons of a slightly lower or higher frequency than normal can cause excitation or de-excitation. This translates to a broadening of the line profile into a Debye line shape. In such a collision-dominated environment, 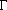= 2 /t_c, where t_c is the mean time between molecular collisions.