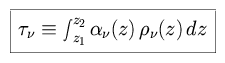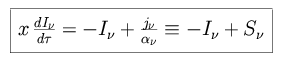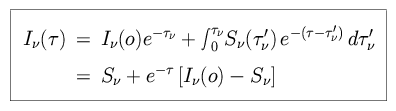Radiative Transfer in an Atmosphere
Radiation is the transport of energy via the absorption and
re-emission of photons. When the primary mechanism of energy transport in an
atmosphere is radiation, the temperature-pressure profile is governed by the
equations of radiative transport. The change in intensity, dI , due to absorption and emission
within a cloud of gas is equal to the difference in intensity between emitted
and absorbed radiation. We define j
, due to absorption and emission
within a cloud of gas is equal to the difference in intensity between emitted
and absorbed radiation. We define j as the emission coefficient due
to scattering and to thermal excitation, and
as the emission coefficient due
to scattering and to thermal excitation, and 
 as the mass extinction
coefficient along a small increment in pathlength ds.
as the mass extinction
coefficient along a small increment in pathlength ds.
Absorption (including stimulated emission, which we can think of as
negative absorption), and scattering both contribute to the extinction:

 =
=

 +
+

 ,
where
,
where

 is the mass absorption coefficient and
is the mass absorption coefficient and

 is the mass scattering coefficient.
is the mass scattering coefficient.
We define z to be the direction of the normal to the surface of a
planet, and  to be the angle
between s and z. It follows that ds = sec
to be the angle
between s and z. It follows that ds = sec  dz. Introducing the variable x =
cos
dz. Introducing the variable x =
cos  , we define the optical
depth
, we define the optical
depth  as follows.
as follows.  is simply the integral along the vertical
pathway of the extinction.
is simply the integral along the vertical
pathway of the extinction.
The change in intensity can be written as
where S is
defined as the ratio of j
is
defined as the ratio of j over
over 
 .
For the case
.
For the case  = 0 (x = 1), this
simplifies to the following. When S
= 0 (x = 1), this
simplifies to the following. When S does not vary with optical depth,
it can be extracted from the integrand (second line). For the general case of
arbitrary
does not vary with optical depth,
it can be extracted from the integrand (second line). For the general case of
arbitrary  , we would replace
, we would replace
 by
by  / x (the slant optical depth).
/ x (the slant optical depth).
If 
 >> 1, then I
>> 1, then I = S
= S and the intensity of the emission is
completely determined by the source function. If
and the intensity of the emission is
completely determined by the source function. If 
 << 1, then I
<< 1, then I = I
= I (o) and the intensity of the
radiation is defined by the incident radiation.
(o) and the intensity of the
radiation is defined by the incident radiation.
 , due to absorption and emission
within a cloud of gas is equal to the difference in intensity between emitted
and absorbed radiation. We define j
, due to absorption and emission
within a cloud of gas is equal to the difference in intensity between emitted
and absorbed radiation. We define j as the emission coefficient due
to scattering and to thermal excitation, and
as the emission coefficient due
to scattering and to thermal excitation, and 
 as the mass extinction
coefficient along a small increment in pathlength ds.
as the mass extinction
coefficient along a small increment in pathlength ds.
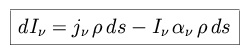


 to be the angle
between s and z. It follows that ds = sec
to be the angle
between s and z. It follows that ds = sec  as follows.
as follows.