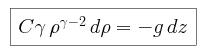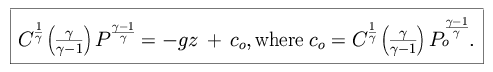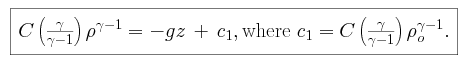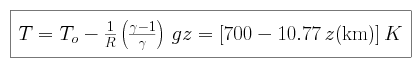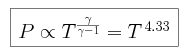Modeling the Venusian Atmosphere
Let us consider the behavior of the atmosphere of Venus within the troposphere
(the lowest level), to get some practice employing both hydrostatic
equilibrium and the ideal gas law.
Near to the planetary surface:
| g | = | 887 | cm per second squared |
| To | = | 700 | K |
| Po | = | 96 | bars |
and the gravitational force g is roughly constant over the regime of
interest. The atmosphere is 96% CO2, so we will ignore the trace
elements.
-
The gas pressure follows the ideal gas law:
where R = 1.9 × 106 cm2 sec-2
K-1 for CO2.
- We invoke hydrostatic equilibrium,
- We are modeling the troposphere, a region where convection dominates,
so we can assume that the pressure is adiabatic, and thus that for some constant C
We begin by combining the expression for adiabatic pressure with the condition
of hydrostatic equilibrium, and find that the pressure P can be
expressed as
and the density 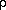 as
as
We integrate our expressions and apply our surface boundary condition to find
that
and
We can then use the ideal gas law to find an expression for temperature as a
function of height above the surface.
The tropopause defines the upper edge of the troposphere, where the atmosphere
becomes transparent to infrared radiation. At a temperature of 233 K, we can
solve for the height to find a value of 43 km (versus 17 km on Earth).
We can then estimate the pressure at this level. Using the scaling relation
between pressure and temperature, we deduce that
and the pressure at the tropopause is 0.82 bars. Though the surface
conditions of Venus are very different from those on Earth, it is interesting
to note that there exists an atmospheric layer with pressure and temperature
conditions quite comparable to those of the Earth's tropopause.
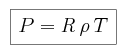
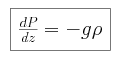
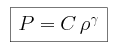
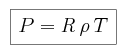
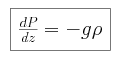
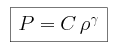
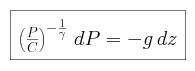
 as
as