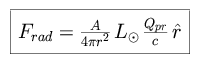
Solar radiation can act as a significant force for small (less than a meter) particles in the solar system. In the non-relativistic case,
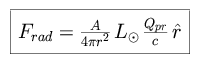 |
where A is the cross-sectional area of the particle presented to the Sun, r is the distance between the particle and the Sun, and Qpr is the radiation pressure coefficient, relating absorption and scattering, equal to unity for a perfectly absorbing sphere. This force acts in opposition to the gravitational attraction of the Sun.
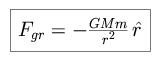 |
Qpr drops to zero for particles of radius significantly less than a micron, following the peak in the visible solar spectrum, and produces a negligible force for larger particles.
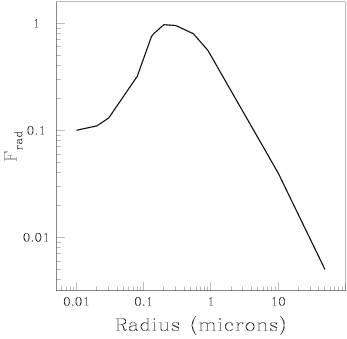 |
| Radiation pressure, Frad, has a significant effect on particles in the range 0.1 to 1 micron. [NMSU, N. Vogt] |
We define the ratio of the two forces as 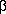 , and evaluate its dependencies. For
a particle of radius R,
, and evaluate its dependencies. For
a particle of radius R,
 |
Note that 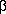 is
independent of the distance r between the Sun and the particle!
The total force can be expressed as follows.
is
independent of the distance r between the Sun and the particle!
The total force can be expressed as follows.
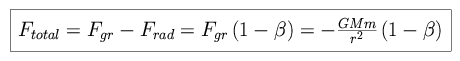 |
Small particles will escape the solar system if 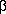 is greater than unity. For dust
particles released from bodies on Keplerian orbits with no eccentricity, we
use the Virial Theorem to calculate the critical value of
is greater than unity. For dust
particles released from bodies on Keplerian orbits with no eccentricity, we
use the Virial Theorem to calculate the critical value of 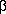 . We begin by calculating the orbital
velocity of the particle.
. We begin by calculating the orbital
velocity of the particle.
 |
We contrast this with the velocity needed to escape the solar system. To move a particle from a radius r to a far distance,
 |
Equating the two, we find the necessary condition for escape.
 |
Consider comet tails, which point away from the Sun due to radiation pressure, yielding a curved tail as the comet travels in space.