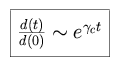
Stability: We define stability within the solar system as a state wherein the orbits of bodies remain well separated, and the planets will remain bound to the Sun for an infinite amount of time.

Chaos: Two trajectories that are arbitrarily close in phase space will diverge exponentially with time. In a chaotic system, the timescale for divergence is independent of the precise values of the initial conditions. We can characterize the deviation between the two trajectories as d, where

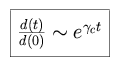The scaling variable 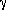_c is the Lyapunov coefficient, and we define its inverse to be the Lyapunov timescale, t_c. Strictly speaking, the system is so sensitive to initial conditions that detailed, long-term behavior is lost within several iterations of this characteristic timescale. We expect a 100% discrepancy within 20 t_c for a change of 10^-10 in initial conditions. For Terrestrial planets, t_c is roughly 5 Myr, a relatively short amount of time that implies significant disorder within 100 Myr (contrast this with t_c = 20 Myr for Jupiter). The timescale for large changes in principal orbital elements, however, is often many orders of magnitude larger than t_c. Furthermore, chaos can be strongly constrained by patterns of resonance.

Consider the case of a simple one-dimensional harmonic oscillator - our friend the spring. We can express the equations of motion as

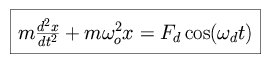where a force F_d drives a mass m which oscillates at frequency _o, at a driving frequency _d.

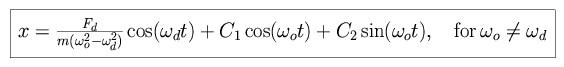This can produce a large-amplitude, long period response if _o is roughly equal to _d, even if the amplitude of the driving force is small. For the case _o = _d, the motion is quite different.

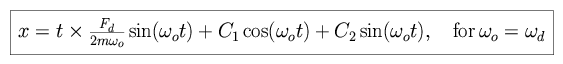This resonant driving force can produce secular (steadily increasing, not periodic) growth. The simplest resonances to visualize are mean motion resonances, for which the orbital periods of two bodies form a ratio of the form

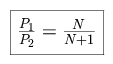where N is an integer. Well-known examples of resonances found in the solar system include the following.

• Europa orbits Jupiter twice as often as does Ganymede.
• Io orbits Jupiter twice as often as does Europa.
• Conjunction occurs at perijove for Io.
• The Trojan asteroids, located at the L4 and L5 points in the Sun - Jupiter system, have a 1:1 resonance with Jupiter.
• The Hilda asteroids have a 3:2 resonance with Jupiter.
• Asteroid 5261 lies at the L4 point for the Sun - Mars system.
• Spiral density and bending waves occur in Saturn's rings at many resonances with the orbital periods of the neighboring moons.

The effect of one body on a neighboring object can be calculated by evaluating the potential as the sum of (1) the Keplerian motion about the Sun, (2) a disturbing function R_dist made up of direct terms for the pairwise interaction, and (3) indirect terms associated with the back-reaction of the bodies on the Sun. For the case of two bodies of mass much less than their primary,

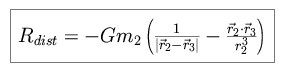The rough limit to the range of influence for a planet, or a moon, of mass m₂ in orbit around a primary of mass m₁ is defined as the extent of the Hill sphere:

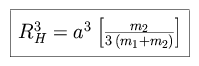A test particle at the edge of the Hill sphere will experience a gravitational force from the planet equal in magnitude to the difference in the tidal force from the Sun on the planet and on the test particle. It extends to the radius of the L1 Lagrange Point, and in the limit where m₂ << m₁ it is equivalent to the Roche lobe (known to us in the context of binary star mass transfer).