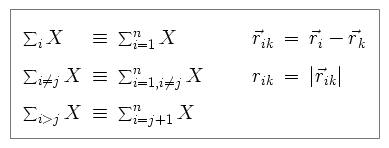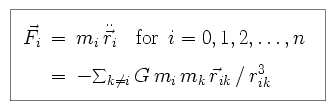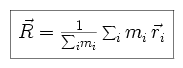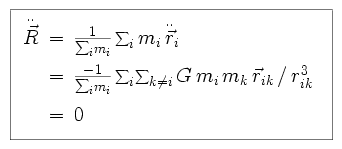Consider the n body problem, with gravity as the sole particle-particle interaction force. We first examine the linear momentum, P. We begin with a few definitions of nomenclature.

We then evaluate the force on the individual particles, numbered i = 1 through n. This is just the sum of the individual gravitational interactions between particles.

We next define R as the movement of the center of mass of the entire system, and consider its derivative with respect to time, i.e. the forces upon it.

This is because we evaluate the double sum over i and k, which adds to zero as r_ik = - r_ki (all terms cancel). This tells us that the velocity of the center of mass is constant, and thus the net linear momentum is a conserved quantity.