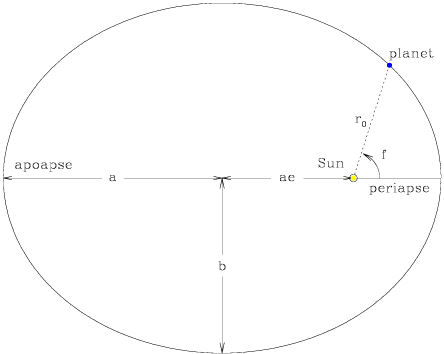
The three principal orbital elements define the scale, the shape, and the orientation of an orbit.

• a: the semimajor axis of the ellipse
• e: the eccentricity of the ellipse
• i: the inclination of the orbital plane with the reference plane (see below)

The semiminor axis, b, is defined by the combination of a and e; b² = a²(1 - e²), while r_o is the instantaneous distance between the planet and the central mass. The apoapse and periapse (or aphelion and perihelion, for solar planets) are the positions of farthest and closest approach to the central mass, while the true anomaly f is the angle formed between r_o and r_o at periapse. By convention, prograde satellites are defined to have inclination angles between 0° and 90°, while retrograde satellites are inclined between 90° and 180°.

[NMSU, N. Vogt]

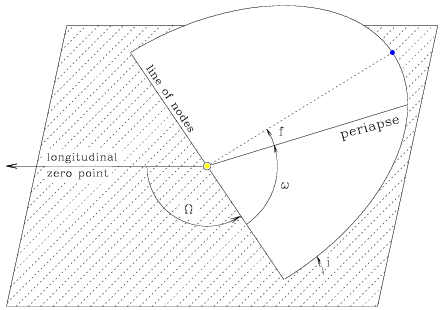
The remaining three orbital elements uniquely specify the orbital position relative to a reference plane, typically the ecliptic (the orbital plane of the Earth about the Sun) for solar objects, or in other cases either the equatorial plane of the most massive body in the system or the plane perpendicular to the vector of the total angular momentum of the system.

The line of intersection between the orbital and reference planes is defined as the line of nodes; the point along this line where the satellite passes upward through the reference plane is the ascending node, in the foreground of the following figure, and the companion point in the background where it passes downward is (wait for it) the descending node. The angle between an arbitrary zero point in the reference plane (defined by the position of the Sun and Earth on the vernal equinox for our solar system) and r_o at the ascending node is 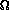, the longitude of the ascending node. The angle between r_o at the ascending node and r_o at periapse, is , the argument of periapse.

• f: the true anomaly (see above)
• : the longitude of the ascending node
• : the argument of periapse

[NMSU, N. Vogt]