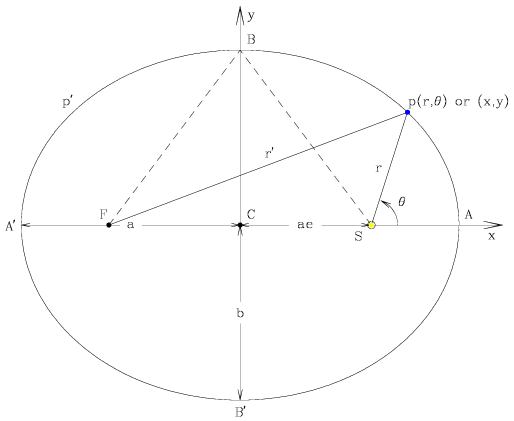
Kepler's First Law
The orbit of each planet is an ellipse with the Sun at one focus.
An ellipse is defined as the locus of all points such that the sum of the
distances from two foci to any point on the ellipse is a constant. Below we
see the elliptical orbit of a planet, P, with the Sun, S, at one
of the foci. The other focus, F, is often called the empty focus. From
the definition of an ellipse, we know that
r + r´ = 2a
 |
| [NMSU, N. Vogt] |
Recall the equation for an ellipse in Cartesian coordinates:
(x/a)2 +
(y/b)2 = 1
This reduces to the equation of a circle when a = b.
We define the following properties of the ellipse.
- major axis - the line AA´, where A
and A´ are the vertices of the ellipse.
- semi-major axis - the lines CA and CA´, where
C is the center of the ellipse. For each point P on the ellipse
at a distance r from focus S, there is a symmetrical point
P´ a distance r´ from S - the average of
these distances is (r + r´) / 2 = a. This result
holds for any arbitrary but symmetrical pair of points. Hence the semi-major
axis is equal to the mean distance from the Sun of a planet in an elliptical
orbit.
- minor axis - the line BB´.
- semi-minor axis - the lines CB and CB´. If
a and b denote the lengths of the semi-major and semi-minor
axes, respectively, then using the dashed lines (r = r´ =
a) and the Pythagoras theorem, we find b2 =
a2(1 - e2), where e is the
eccentricity of ellipse.
- eccentricity - the ratio CS / CA. The eccentricity
gives an idea of how elongated the ellipse is. If the ellipse is a circle,
e=0, since S and F are coincident with C. The
other limit for e is 1, obtained when the ellipse is so narrow that the
empty focus is removed to infinity. The distance from each focus to the
center of the ellipse is ae.
- perigee - when the planet, P, is at A. It is then
nearest the star since SA = CA - CS = a -
ae = a (1 - e). If the gravitating body is the Sun, this
point is known as perihelion.
- apogee - when the planet, P, is at A´. It is
then farthest from the star since SA´ = CA´ +
CS = a + ae = a (1 + e). If the
gravitating body is the Sun, this point is known as aphelion.
- true anomaly - the angle ASP.

