Celestial mechanics is the study of the orbits of celestial bodies, such as planets, satellites, comets, asteroids and spacecraft. We begin with a few definitions of terms.
 |
| [NMSU, N. Vogt] |
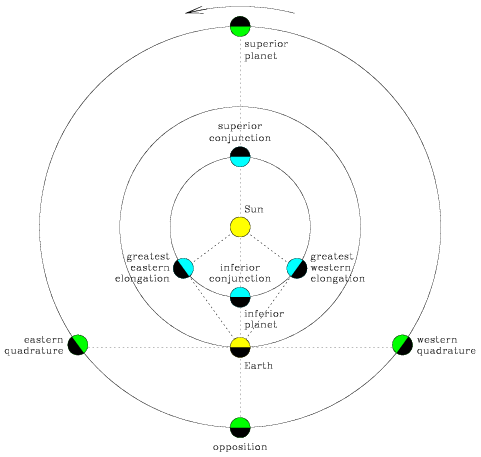
The planets all shine by reflected sunlight, and so half of a planet is always sunlit while the other half is dark. The fraction of the sunlit hemisphere seen from the Earth, however, varies with the planetary configuration. Because of this, the variety of phases exhibited by superior planets differ markedly from those of the inferior planets. The new phase occurs when we see only the dark hemisphere. This can only occur at inferior conjunction and so can never be seen on the superior planets. Full phase, when the entire sunlit hemisphere of a planet is visible, occurs when a planet is in opposition and so can only ever be observed on a superior planet (the inferior planets at superior conjunction also show a full phase, but this is lost in the glare of the Sun). The superior planets can never be observed in crescent phase, when less than half of the observable hemisphere is sunlit, whereas inferior planets can. Superior planets are almost always observed in gibbous phase, when more than half of the planet appears sunlit. Inferior planets also exhibit gibbous phases.
 |
| [NMSU, N. Vogt] |
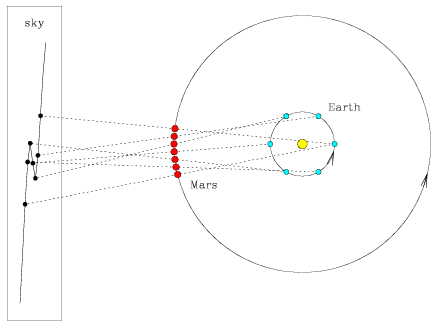
The farther a planet lies from the Sun, the slower it moves around the Sun. When the Earth and another planet pass each other on the same side of the Sun, the planet appears to retrace its path for a short while (retrograde motion) and then continue in its original direction (prograde motion). As we view the planet from the moving Earth, our line of sight reverses the apparent motion of the planet twice. When the orbits of the Earth and the planet are not co-planar, the motion of the planet in the sky appears as a loop.
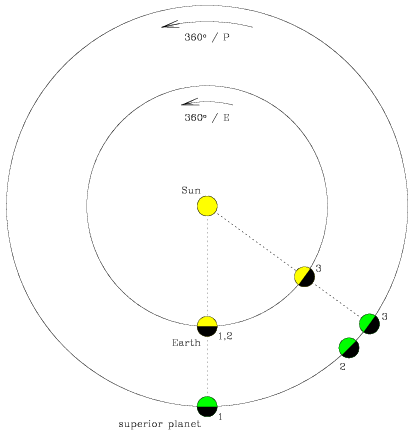
The synodic period, S, is the time it takes the planet to return to the same position in the sky relative to the Sun, as seen from the Earth. The sidereal period, P, is the time it takes the planet to complete one orbit of the Sun (the orbital period). If the Earth's sidereal period is E, the Earth moves at the rate of 360°/E (in degrees per day) in its orbit, while a planet's rate of angular motion is 360°/P as viewed from the Sun. Below, the Earth moves from position 1 to position 2 after one orbit and then has S - E days to catch up with the superior planet at opposition again (position 3). During this time, the superior planet has moved from position 1 to position 3. So the Earth must traverse the angle (S - E) x (360°/E) in the same time that the superior planet traverses the angle S x (360°/P). Because of this,
For an inferior planet, the Earth is a superior planet, and so we interchange E and P such that
1/S = 1/P - 1/E (inferior)
1/S = 1/E - 1/P (superior).
It is now a simple matter to time how long it takes to see, for example, two successive oppositions of a (superior) planet, S, and to determine the length of the year, P, on any planet in the solar system.
 |
| [NMSU, N. Vogt] |