[NMSU, N. Vogt]

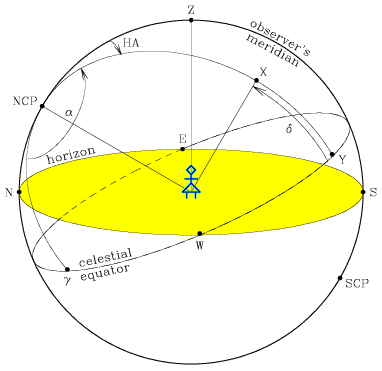
Because the altitude and azimuth of a star are constantly changing, it is not possible to use them in a catalog of positions. A more convenient coordinate system for such purposes is one based on the celestial equator and the celestial poles, defined in a similar manner to latitude and longitude on the surface of the Earth. In this equatorial system, the analogue of latitude is the declination, 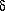. The declination of a star is its angular distance in degrees measured from the celestial equator along the meridian through the star. It is measured north and south of the celestial equator and ranges from 0° at the celestial equator to 90° at the celestial poles, being taken to be positive when north of the celestial equator and negative when south. In the figure above, the declination of the star X is given by the angle between Y and X.

The analogue of longitude in the equatorial system is the hour angle, HA. Defining the observer's meridian as the arc of the great circle which passes from the north celestial pole through the zenith to the south celestial pole, the hour angle of a star is measured westwards from the observer's meridian (for both northern and southern hemisphere observers) to the meridian through the star. Because of the rotation of the Earth the hour angle increases uniformly with time, increasing from 0° to 360° in 24 hours. The hour angle of a particular object is therefore a measure of the time since it crossed the observer's meridian - hence the name. For this reason it is often measured in hours, minutes and seconds of time rather than in angular measure (when observing, for example, one might track HA from -6 to +6 hours). The hour angle of the star X is given by the angle Z-NCP-X. Note that all stars attain their maximum altitude above the horizon when they transit (or attain upper culmination, in the case of circumpolar stars) the observer's meridian.

The declination of a star does not change with time. The hour angle does, and hence it is not a suitable coordinate for a catalog. This problem is overcome in a manner analogous to the way in which the Greenwich meridian has been selected as the zero point for the measurement of longitude. The zero point chosen on the celestial sphere is the first point of Aries, 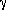, and the angle between it and the intersection of the meridian through a celestial object and the celestial equator is called the right ascension (RA) of the object. Right ascension is denoted by the Greek letter and is measured from 0 to 24 hours along the celestial equator eastwards from the first point of Aries (in the opposite direction to that in which hour angle is measured). Like the definition of hour angle, this convention holds for observers in both northern and southern hemispheres. The right ascension of the star X is given by the angle 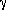-NCP-Y.

Most modern research telescopes do not use equatorial mounts due to their high cost and low stability. This is at the expense of the simplicity of telescope tracking - an equatorially-mounted telescope need only move its right ascension axis in order to track the motion of the celestial sphere.

In the above discussions on coordinate systems and the celestial sphere we make the assumption that the stars are fixed on the celestial sphere and never move. For accurate positional work on long timescales, this assumption does not hold - the stars do move on the celestial sphere. The Earth's axis of rotation precesses slowly in space, like a spinning top, due to the gravitational attractions of the Sun and Moon on the rotating, non-spherical Earth. Because of this, the north celestial pole traces out a small circle with a radius equal to the obliquity of the ecliptic, . This also causes the celestial equator to move, and thus the first point of Aries is not a fixed reference point; it moves gradually backwards along the ecliptic, at a rate of 50 arcseconds per year, and is currently in the neighboring constellation of Pisces. This motion is known as the precession of the equinoxes and it means that even right ascension and declination are not quite fixed coordinates and catalogs of star positions have to specify the date (e.g. 1950 or 2000) to which they refer. More precisely, the coordinate frame used for catalog positions is defined by the position of the vernal equinox (the first point of Aries) on a particular date. The pole takes some 26,000 years to make one revolution, but as the effect of precession is much larger than the uncertainties in the positions of objects, positional measurements must be corrected for precession.

Precession only rotates the reference frame, and has no effect on the relative positions of stars. However, stars are not stationary in space; they move around the center of the Galaxy in different orbits, and so nearby stars have measurable motions relative to the Sun. The projection of these motions onto the celestial sphere is known as proper motion, , and it does cause changes in the relative positions of stars. It is therefore not sufficient to give a single catalog position for a star, since it will change as a result of proper motion. For stars with significant proper motion, it is necessary to specify both the proper motion and the date of the observation (known as the epoch), as well as the catalog position and the equinox to which it refers. If no epoch is given for a position, it is assumed that the epoch is the same as the equinox of the reference frame.

There are a number of other, generally smaller, corrections astronomers need to make to the coordinates of an astronomical object before doing accurate positional work. These include atmospheric refraction, stellar aberration and nutation.