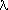Astronomy 505

Fourier Analysis

For a smoothly varying function F(z) with period

, we can express the function as a superposition of sine and cosine terms. (For a bounded function where F(z=0) = F(z=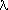

) = 0, sine terms alone will suffice.)

where B_o, A_n, and B_n are the Fourier coefficients. We find the form of B_o as follows, by integrating our expression for F(z) over a full period. For an arbitrary value of z which we will call z₁,

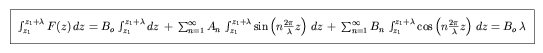and we deduce that

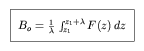taking advantage of the symmetry of both sine and cosine functions over a full period:

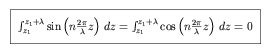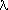To find A_m, where m is any value of n, we multiply our expression for F(z) by sin (m 2 z / ) and again integrate over a complete period.

leading to

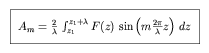making use of symmetry and the fact that

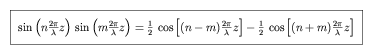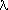To find B_m, we multiply our expression for F(z) by cos (m 2 z / ) and again integrate over a complete period.

leading to

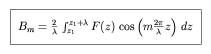again making use of symmetry, and the fact that

Test your comprehension:

What are the values of the Fourier coefficients for the case where F(z) is a square wave?

Are the Fourier components a good set of basis vectors to use to express this particular function?

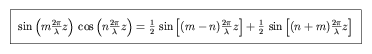You should be able to determine which coefficients are non-zero simply by sketching a few quick curves.